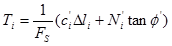Muri di Sostegno Stati Limite V.2020 - in cemento armato, a gravità ..
Software per il calcolo dei Muri di Sostegno.
Caratteristiche Geometriche, Caratteristiche Materiali, Analisi strutturale,
Verifiche Stati Limite Ultimi : ribaltamento, scorrimento, carico limite, stabilità globale
PressoFlessione e Taglio,
Verifiche Stati Limite di Esercizio , Stati Limite di Danno
Relazione di Calcolo, Tabulato di Calcolo, Relazione sui Materiali,
Esecutivi di cantiere BMP, DXF, DWG
|
Software di Calcolo Muri di Sostegno |
calcolo muro di sostegno ntc 2018muri di sostegno in cemento armato muri di sostegno a gravità relazione di calcolo tabulato di calcolo relazione sui materiali relazione geotecnica relazione sulle fondazioni piano di manutenzione esecutivi di cantiere
|
Il software, Muri di Sostegno, consente di effettuare il calcolo dei muri di sostegno sia in cemento armato che a gravità, con base di fondazione rettangolare posta su un piano orizzontale, con il metodo di verifica agli stati limite di cui al D.M. 17/01/2018.
Inserite le dimensioni del muro, specificati i parametri sismici e le caratteristiche dei materiali, il programma consente di effettuare velocemente il calcolo dello stesso, determinando le spinte generate dal terreno posto a tergo, le forze sismiche che si ingenerano sul muro in base a quanto stabilito dalla normativa, ed effettuando le necessarie verifiche di stabilità.
Se il muro è in cemento armato, oltre ad effettuare il calcolo delle spinte e le verifiche di stabilità, il programma effettua le verifiche di resistenza mediante il calcolo delle armature e la verifica a presso-flessione e taglio della fondazione e del paramento.
Una volta effettuato il calcolo del muro, consente di effettuare velocemente il disegno degli esecutivi di cantiere.
Index
|
|
Dati Muro
Selezionando il comando “Dati Muro” si attiva una finestra di dialogo in cui è possibile specificare i dati relativi alla geometria del muro, alle caratteristiche dei terreni ed ai carichi applicati.
Geometria Muro
Consente di specificare le dimensioni del muro:
- - Spessore;
- - Altezza;
- - Pendenza paramento esterno;
- - Angolo paramento interno;
- - Spessore Fondazione;
- - Larghezza Mensola interna;
- - Larghezza Mensola esterna;
- - Profondità Piano di Posa.
In automatico determina Spessore al Piede del paramento e Larghezza Fondazione, inoltre in fase di inserimento dati esegue il disegno del muro, evidenziando il dato che si sta specificando.
|
|
Dati Terreno
Nella finestra di dialogo "Dati Muro", selezionandola scheda "Terreno" è possibile specificare le caratteristiche del terreno in elevazione ed in fondazione.
|
|
- Peso Specifico del Terreno- - Angolo di Attrito
- - Coesione
- - Angolo di Inclinazione terrapieno
- - Profondità Falda
Tali dati oltre ad essere necessari per eseguire il Calcolo delle Spinte e quindi per le verifiche di resistenza del muro, vengono riportati nella relazione geotecnica e nella relazione sulle fondazioni.
In presenza di acqua, è necessaro specificare la Profondità della Falda , che come si evince dalla figura indica la quota tra il terreno a monte del muro ed il livello della falda. In questo caso il software oltre a determinare la spinta dovuta al terrapieno determinerà pure la spinta dovuta all'acqua.
Carichi
Nella finestra di dialogo "Dati Muro" , selezionando la scaheda "Carichi" è possibile specificare gli eventuali carichi applicati al muro di sostegno (sovraccarico, forze concentrate, ecc.) oltre alle spinte del terreno.
|
|
- - Sovraccarico distribuito e relativa distanza di appliicazione
- - Forza Verticale concentrata in sommità
- - Forza Orizzontale concentrata in sommità
- - Momento Flettente
- - Forza Orizzontale applicata sul paramento e relativa distanza dalla base
Materiali
Selezionando il comando “Impostazioni - Caratteristiche Materiali” si attiva una finestra di dialogo in cui è possibile specificare il tipo di materiale con cui è realizzato il muro di sostegno.
Muri in Cemento Armato
E' possibile specificare il tipo di Calcestruzzo e le relative caratteristiche meccaniche.
Selezionando la Classe di resistenza vengono determinate in automatico le caratteristiche meccaniche del calcestruzzo (Resistenza caratteristca, valori medi, resistenza di progetto).
|
Caratteristiche Materiale Calcestruzzo |
E' possibile specificare il tipo di Acciaio e le relative caratteristiche meccaniche:
|
Caratteristiche Materiale Acciaio |
Muri a Gravità
E' possibile specificare il tipo di materiale con cui è realizzato il muro a gravità e le relative caratteristiche meccaniche:
|
Caratteristiche Materiale Muro a Gravità |
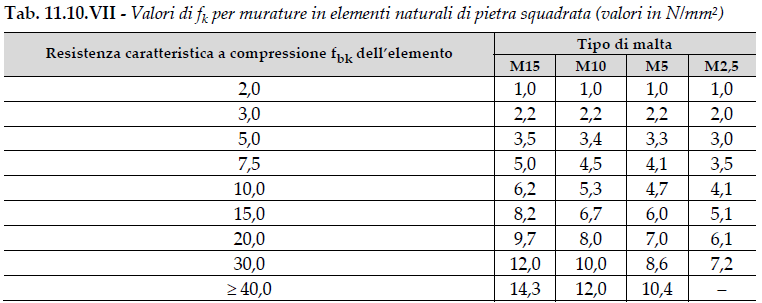
Solo a scopo indicativo, facendo click sul simbolo * adiacente fk, verrà mostrata la Tabella 11.10.VII di cui al D.M. 17/01/2018 indicante i valori della Resistenza Caratteristica a Compressione delle murature in elementi naturali di pietra in funzione della Resistenza Caratteristica a Compressione dle Blocco e del tipo di Malta:
facendo click sul simbolo * adiacente gm, verrà mostrata la Tabella 4.5.II di cui al D.M. 17/01/2018 indicante il coefficiente di sicurezza per alcune tipologie di murature:

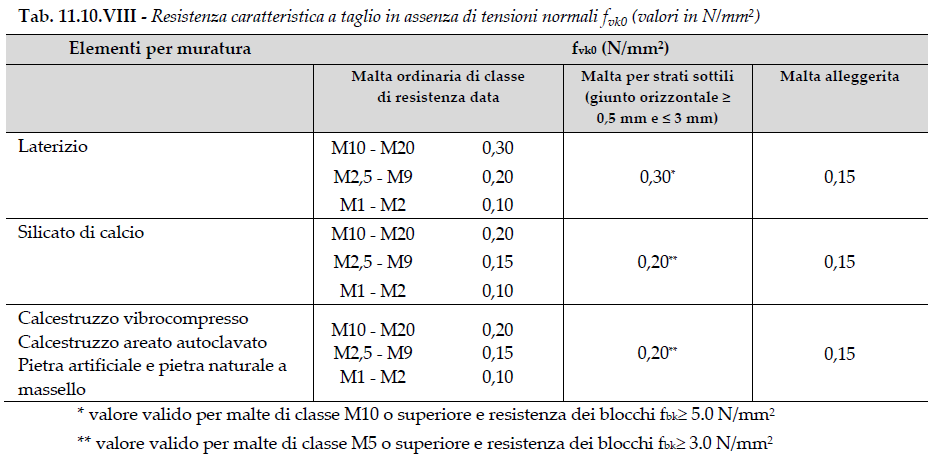
facendo click sul simbolo * adiacente fvko, verrà mostrata la Tabella 4.5.II di cui al D.M. 17/01/2018 indicante i valori della Resistenza Caratteristica a Taglio di alcune murature:
Coefficienti Normativa
Selezionando il comando "Impostazioni" - "Coffeicienti Normativa" è possibile specificare i coefficienti da normativa che devono essere utilizzati per le azioni, per i parametri geotecnici e per le resistenze.
In particolare, si precisa che il software, esegue le verifiche di tipo geotecnico (GEO) e di tipo strutturale (STR), accertando che la condizione (6.2.1) " Ed < Rd " di cui al DM.2018 sia soddisfatta per ogni stato limite considerato, sulla base di quanto impone la normativa al par. 6.5.3.1.1. per le Verifiche agli SLU ed al par.6.5.3.2. per le verifiche agli SLE.
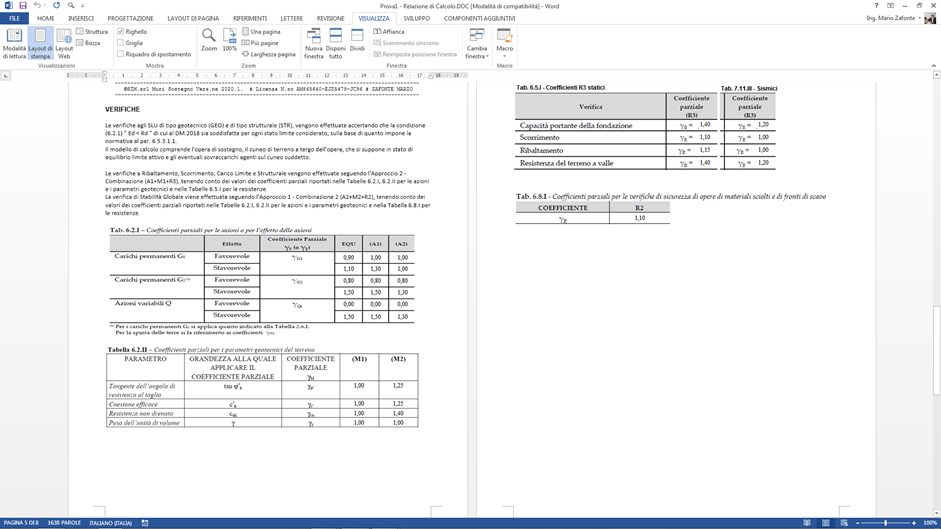
Le verifiche a Ribaltamento, Scorrimento, Carico Limite e Strutturale vengono effettuate seguendo l'Approccio 2 - Combinazione (A1+M1+R3), tenendo conto dei valori dei coefficienti parziali riportati nelle Tabelle 6.2.I, 6.2.II per le azioni e i parametri geotecnici e nelle Tabelle 6.5.I per le resistenze.
La verifica di Stabilità Globale viene effettuata seguendo l'Approccio 1 - Combinazione 2 (A2+M2+R2), tenendo conto dei valori dei coefficienti parziali riportati nelle Tabelle 6.2.I, 6.2.II per le azioni e i parametri geotecnici e nella Tabella 6.8.I per le resistenze.
Il software in automatico propone i valori dei coefficienti di cui al D.M. 17/01/2018.
Se si desidera, effettuare il calcolo di un caso studio, con coefficienti diversi da quelli indicati dalla normativa, è possibile modificare detti coefficienti.
|
|
|
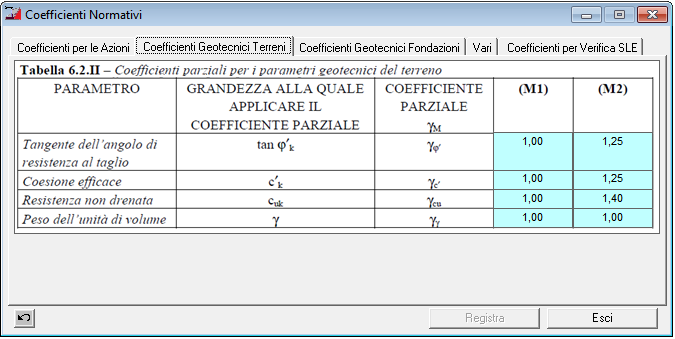
Tabella 6.2.II – Coefficienti per i parametri geotecnici del terreno |
|
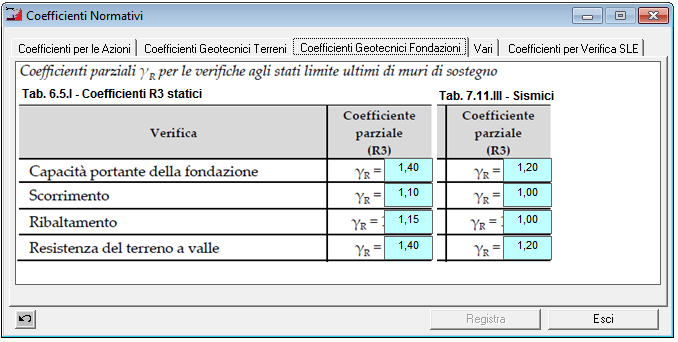
Tabella 6.5.I – Coefficienti per la Resistenza |
|
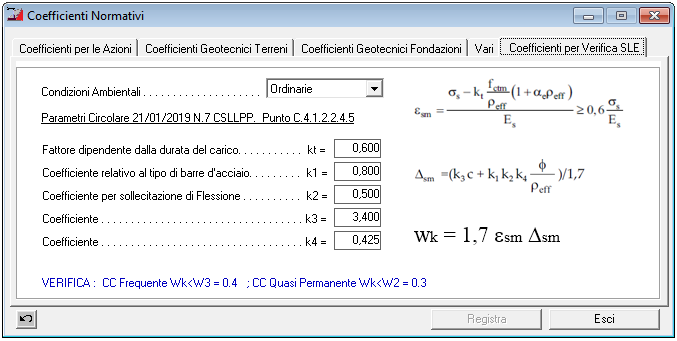
Punto C.4.1.2.2.4.5 Circ. N.7/2019 – Parametri Verifica SLE Apertura Fessure Muri c.a. |
Parametri Sismici
Selezionando il comando “Parametri Sismici e di Calcolo” , si attiva una finestra di dialogo nella quale è possibile specificare i parametri necessari alla verifica sismica del muro, oltre a specificare varie opzioni relativamente alla verifica di stabilità, alle armature minime da porre nel muro in c.a., etc.
|
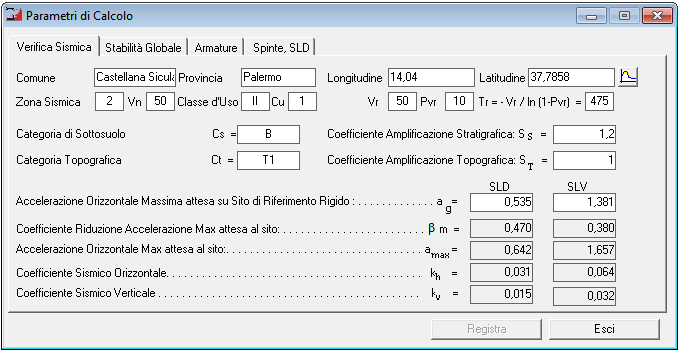
Parametri per Verifica Sismica |
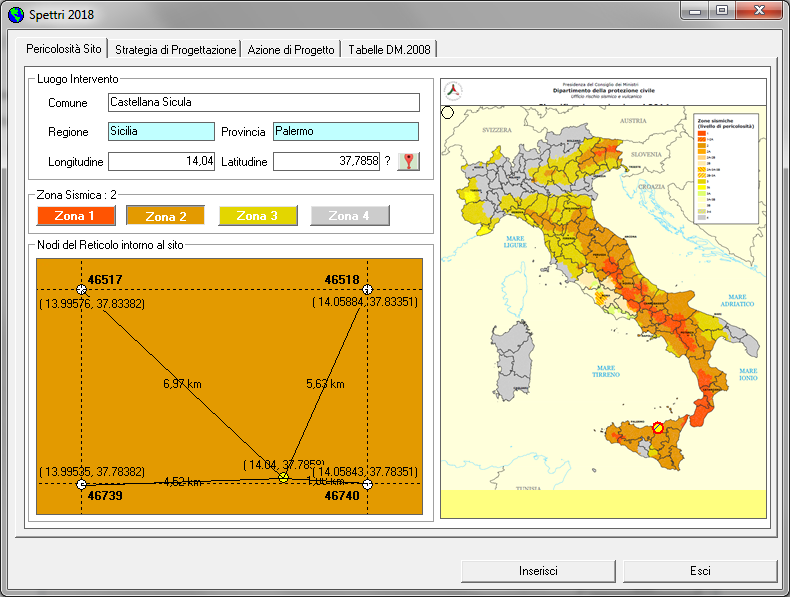
Nella Scheda "Verifica Sismica" è possibile specificare i parametri di pericolosità sismica per il sito in cui ricade la costruzione, sulla base di quanto indicato al par. 3.2 del D.M. 17/01/2018, ad esempio:
Dati Generali
- Provincia : Palermo Comune : Castellana Sicula
- Latitudine : 37,7858 Longitudine : 14,04
- Zona Sismica : 2
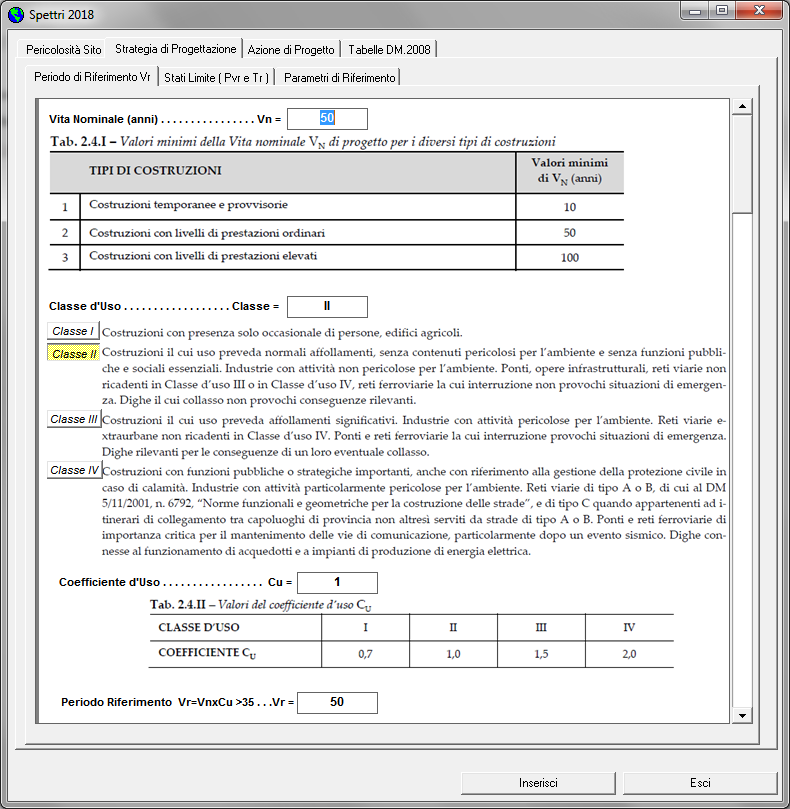
Vita Nominale, Classe d'Uso, Periodo di ritorno
- Vita Nominale Vn = 50 anni
- Classe d'Uso II Coefficiente d'Uso Cu = 1
- Periodo di Riferimento Vr = Vn·Cu = 50 Probabilità Superamento Pvr = 10
- Periodo di Ritorno Tr = - Vr / ln(1-Pvr)=475 anni
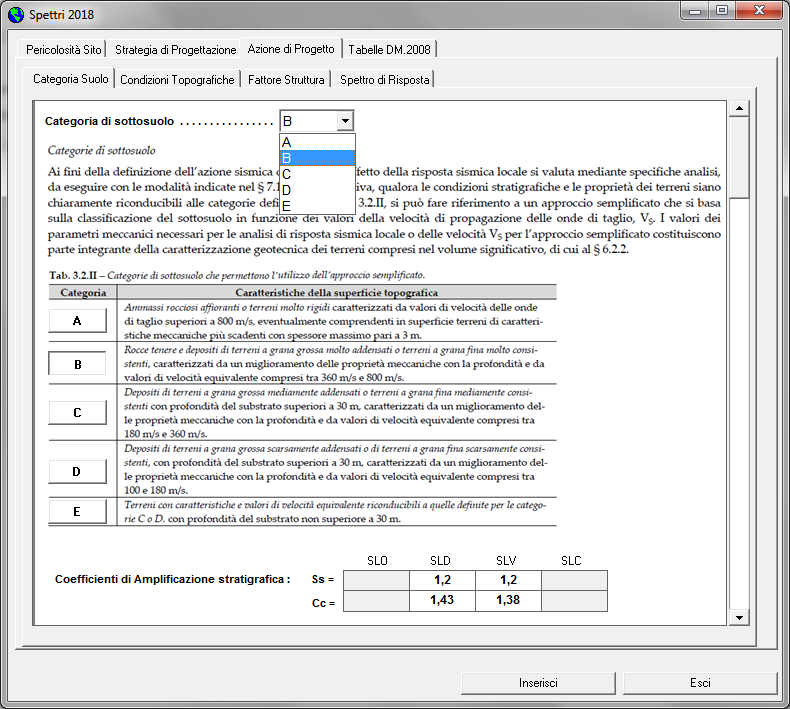
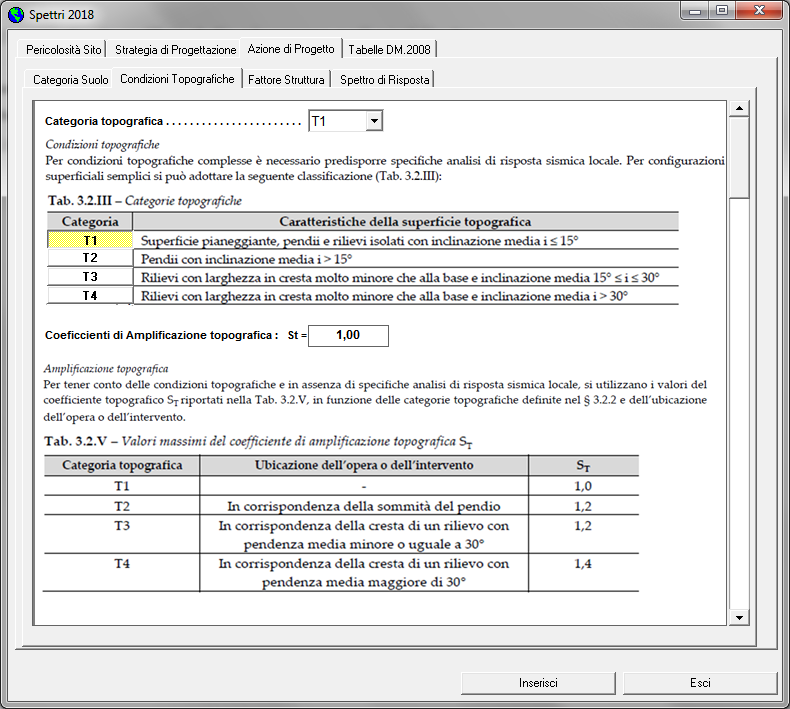
Categorie Sottosuolo e Topografiche
- Categoria sottosuolo B Coef. Amplif. Stratigrafica Ss = 1,2
- Categoria Topografica T1 Coef. Amplif. Topografica St = 1
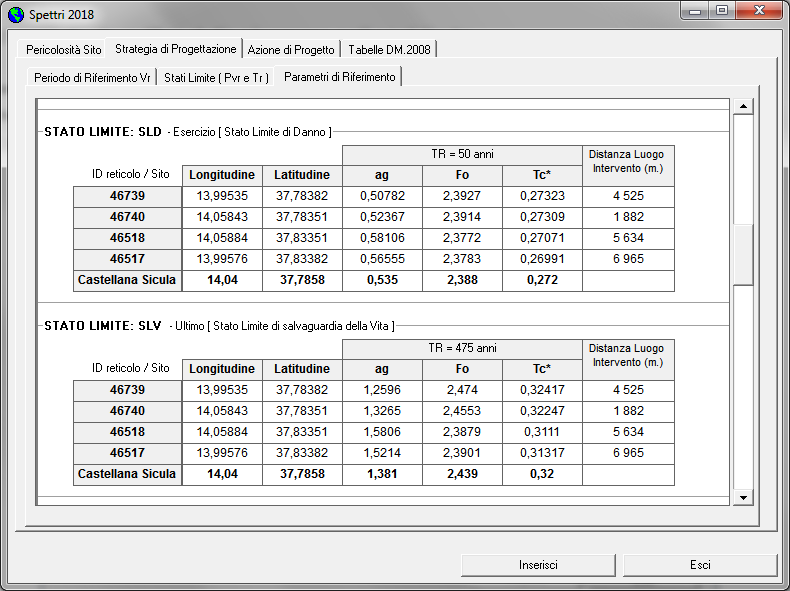
Accelerazione Orizzontale Massima attesa su Sito di Riferimento Rigido
- Stato Limite di Danno ag = 0,535 Stato Limite Salvaguardia Vita ag = 1,381
Specificati tali parametri, il software in automatico calcola i valori di:
- amax = accelerazione orizzontale massima attesa al sito;
-
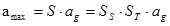
- kh = coefficiente sismico orizzontale
-
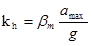
- kv = coefficiente sismico verticale
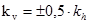
In fase di Calcolo, tali parametri consentiranno il calcolo delle azioni sismiche da applicare al Muro di Sostegno per le Verifiche:
|
Forze di Inerzia Muro |
|
|
| Forze di Inerzia Terrapieno | |
|
| Incremento di Spinta Sismica | |
|
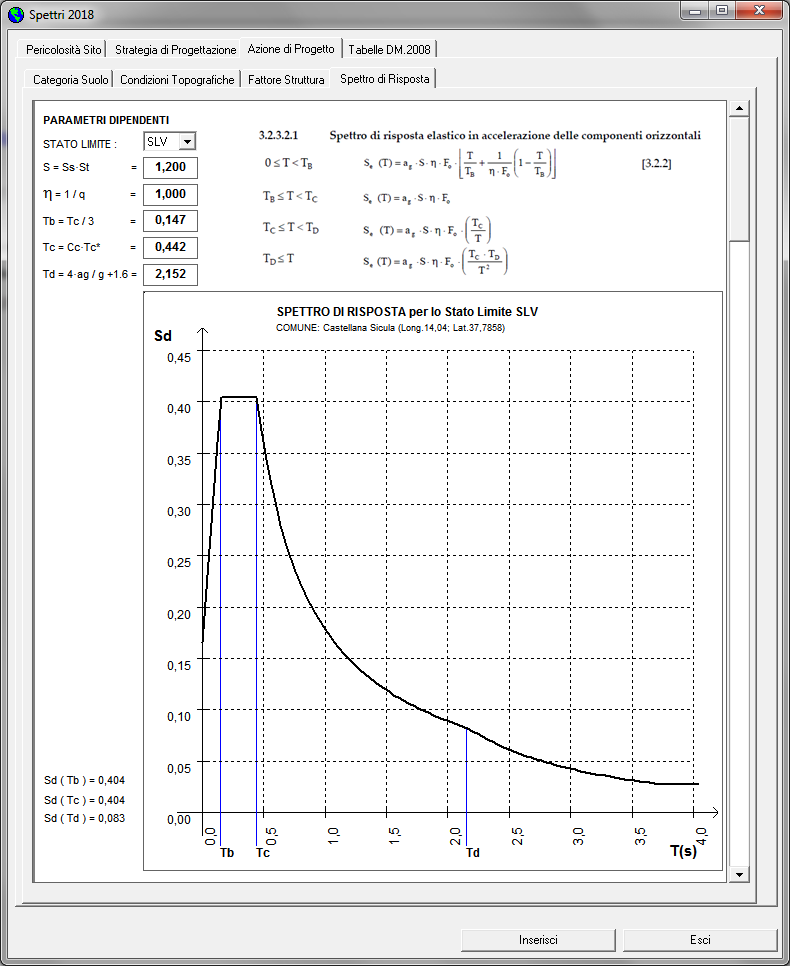
Spettri 2018
Se si desidera , è possibile avviare il modulo “Spettri 2018” il quale consente di inserire i dati suddetti e determinare il valore della Accelerazione Orizzontale Massima attesa su Sito di Riferimento Rigido sia per lo SLD che per lo SLV.
|
Parametri per Verifica Sismica - Luogo Intervento
Vita Nominale, Classe d'Uso, Periodo di Riferimento
Parametri di Riferimento SLD SLV
Categoria Sottosuolo - Coefficienti di Amplificazione Stratigrafica
Categoria Topografica - Coefficiente di Amplificazione Topografica
Spettro di Risposta |
Parametri di Calcolo
Selezionando il comando “Parametri Sismici e di Calcolo” , si attiva una finestra di dialogo nella quale è possibile specificare i parametri necessari alla verifica sismica del muro, oltre a specificare varie opzioni relativamente alla verifica di stabilità, alle armature minime da porre nel muro in c.a., etc.
Opzioni per Verifica Stabilità Globale
Per effettuare la verifica di stabilità globale, il software per default imposta dei parametri quali:
- il numero di conci da considerare per ogni superficie di rottura;
- il numero max di iterazioni che deve eseguire per calcolare il coefficiente Fs;
- il numero di cerchi da considerare per ogni centro:
-
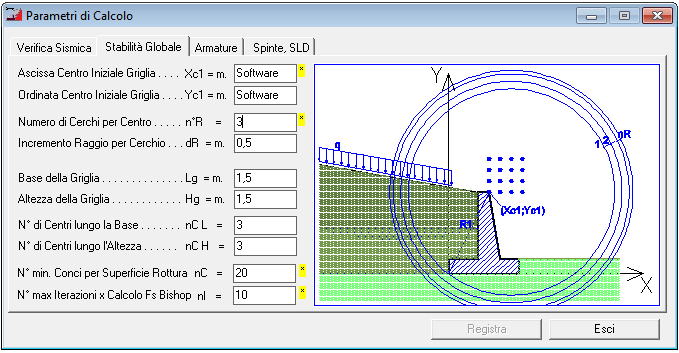
Parametri di Calcolo - Verifica Stabilità Globale
Se si desidera, al fine di aumentare la precisione del calcolo, è possibile modificare detti parametri.
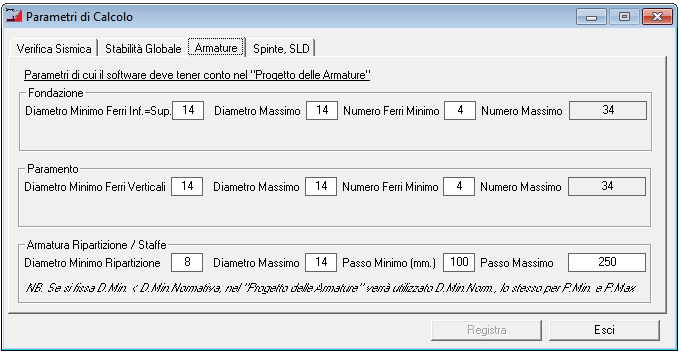
Opzioni per Progetto Armature
Nel caso di muri di sostegno in cemento armato, il software determina in automatico l’armatura minima necessaria affinché siano soddisfatte le verifiche strutturali.
Se si desidera è possibile specificare alcuni parametri di cui il software deve tener conto nel progetto delle armature.
|
Parametri di Calcolo - Armature Muro c.a. |
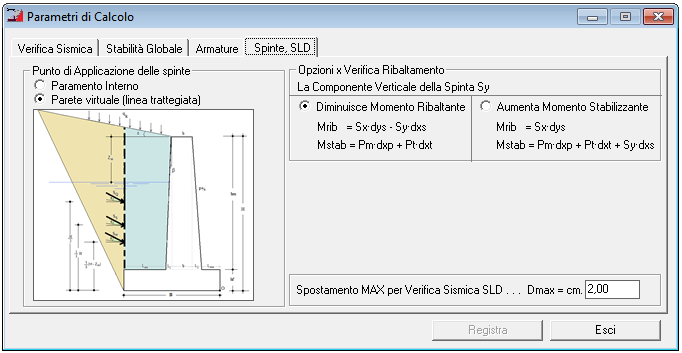
Opzioni per Calcolo Spinte, Verifica ribaltamento e SLD
|
Parametri di Calcolo - Spinte, Verifica ribaltamento e SLD |
Calcolo Spinta Statica
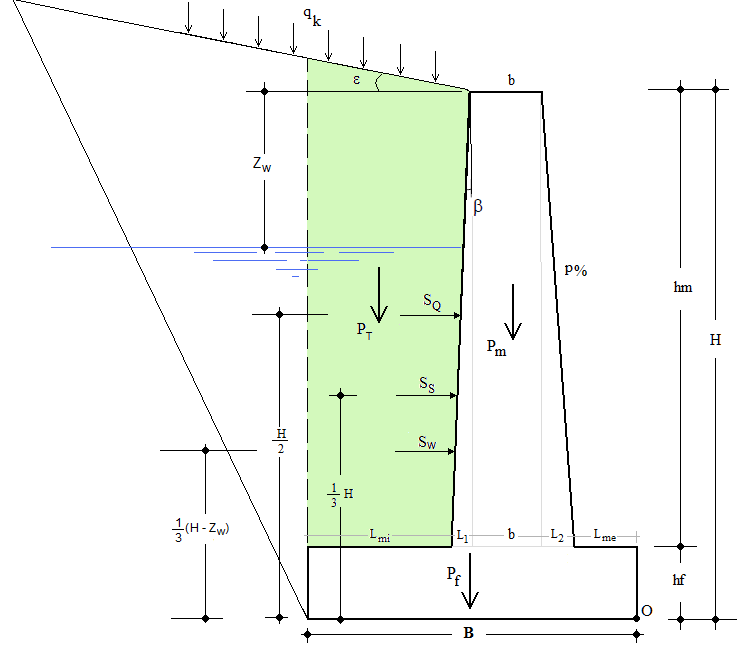
Il calcolo della spinta statica dovuta al terrapieno, al sovraccarico ed all'acqua si basa sulla teoria di Coulomb nell'ipotesi di fondazione rigida e superficie di rottura piana passante per il piede del muro.
Spinta Terrapieno
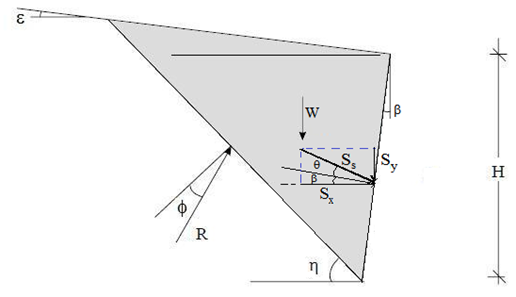
La spinta dovuta al terrapieno, applicata ad un'altezza pari ad 1/3·H, ed inclinata di q rispetto la perpendicolare al paramento interno, risulta:
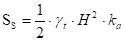
|
Cuneo di Spinta Attiva di Coulomb |
essendo:
gt : il peso specifico del terreno;
H : l 'altezza totale del muro;
Ka : il coefficiente di spinta attiva statica, valutato tramite la seguente espressione,
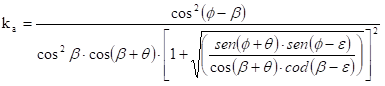
dove:
b = angolo che il parametro interno forma con la verticale;
f = angolo di attrito interno del terreno;
q = angolo di attrito terra - muro;
e = angolo che il terrapieno forma con l'orizzontale.
Spinta dovuta al sovraccarico
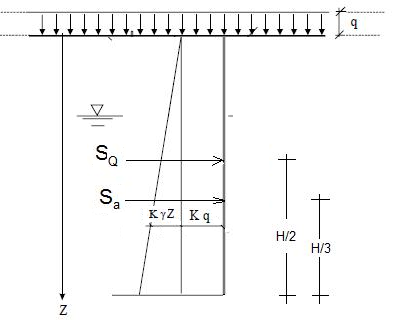
Il sovraccarico Q verticale, uniforme ed infinitamente esteso, genera una spinta sul muro pari a
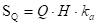
Tale spinta è applicata ad 1/2·H.
|
Spinta dovuta al Sovraccarico |
Spinta dovuta alla pressione interstiziale
La teoria di Coulomb sulla spinta delle terre che abbiamo esaminato si riferisce a terreni asciutti o comunque non sotto falda e quindi con acqua nei pori non in pressione.
Se un terreno è anche solo parzialmente sotto falda, la spinta totale esercitata contro una parete sarà somma di due forze: la prima forza è la spinta esercitata dal terreno, valutata con le formule sopra citate, la seconda forza è la spinta esercitata dall’acqua interstiziale. Quest’ultima si calcola integrando il diagramma delle pressioni interstiziali.
La presenza di acqua in pressione contro una parete di sostegno del terreno determina un forte incremento della spinta totale, pertanto, ove possibile, è sempre opportuno realizzare opere di drenaggio a tergo dell’opera allo scopo di abbattere il livello di falda.
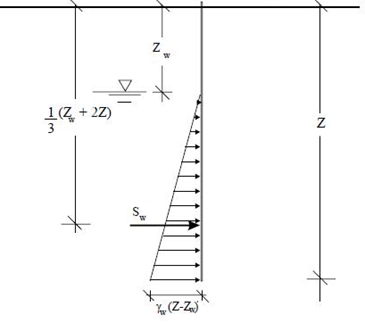
Nel caso particolare, ma frequente, di falda freatica alla profondità Zw si ottiene:
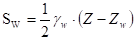
| Tale spinta è applicata a: | 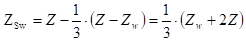 |
|
Spinta Interstiziale |
Calcolo Spinta Sismica
La spinta sismica (dovuta al terrapieno) viene determinata, facendo riferimento al metodo di Mononobe - Okabe.
Detta ε l’inclinazione del terrapieno rispetto all’orizzontale e β l’inclinazione della parete rispetto alla verticale, la spinta S' (statica + dinamica) può determinarsi considerando una inclinazione del terrapieno e della parete pari a:
ε' = ε + q b' = b + q
dove
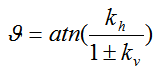 |
nel caso di Livello di falda al di sotto del muro di sostegno |
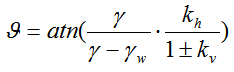 |
nel caso di Terreno impermeabile al di sotto del livello di falda |
| kh , kv | coefficienti sismici orizzontale e verticale, (Vedi Parametri Sismici) |
e risulta:
![]()
essendo:
Ks : il coefficiente di spinta attiva sismica, valutato tramite la seguente espressione,
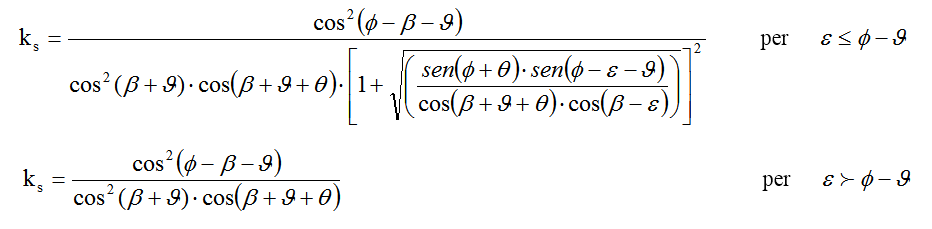
Detta S la spinta calcolata in condizioni statiche l’incremento di spinta da applicare è espresso da: DS = AS' - S
dove il coefficiente A vale:
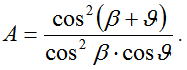
Verifiche Stati Limite Ultimi
Nelle verifiche di sicurezza devono essere presi in considerazione tutti i meccanismi di stato limite ultimo, sia a breve sia a lungo termine.
Gli stati limite ultimi delle opere di sostegno si riferiscono allo sviluppo di meccanismi di collasso determinati dalla mobilitazione della resistenza del terreno, e al raggiungimento della resistenza degli elementi strutturali che compongono le opere stesse.
Verifiche Statiche
Le verifiche statiche vengono eseguite con riferimento ai seguenti stati limite, accertando che la condizione [6.2.1] sia soddisfatta per ogni stato limite considerato:
- SLU di tipo geotecnico (GEO)
- - scorrimento sul piano di posa;
- - collasso per carico limite dell’insieme fondazione-terreno;
- - ribaltamento;
- - stabilità globale del complesso opera di sostegno-terreno;
- SLU di tipo strutturale (STR)
- - raggiungimento della resistenza negli elementi strutturali,
La verifica di stabilità globale del complesso opera di sostegno-terreno viene effettuata, secondo l’Approccio 1 con la Combinazione 2: (A2+M2+R2) tenendo conto dei coefficienti parziali riportati nelle Tabelle 6.2.I e 6.2.II per le azioni e i parametri geotecnici, e nella Tabella 6.8.I per le verifiche di sicurezza di opere di materiali sciolti e fronti di scavo.
Le rimanenti verifiche vengono effettuate secondo l’Approccio 2, con la combinazione (A1+M1+R3), tenendo conto dei valori dei coefficienti parziali riportati nelle Tabelle 6.2.I, 6.2.II e 6.5.I.
Nella verifica a ribaltamento i coefficienti R3 della Tab. 6.5.I si applicano agli effetti delle azioni stabilizzanti.
Tali verifiche vengono effettuate applicando al muro di sostegno i carichi:
- Peso Muro
- Peso terrapieno
- Spinta Statica
- Sovraccarico e Forze esterne
Verifiche Sismiche
Nelle verifiche di sicurezza in condizioni sismiche si controlla che la resistenza del sistema sia maggiore delle azioni nel rispetto della condizione [6.2.1], ponendo pari all’unità i coefficienti parziali sulle azioni e sui parametri geotecnici (§.7.11.1) e impiegando le resistenze di progetto con i coefficienti parziali gr indicati nella tabella 7.11.III.
Per lo stato limite di ribaltamento, inoltre, si utilizzano valori di bm incrementati del 50% rispetto a quelli innanzi indicati e comunque non superiori all’unità.
In particolare, vengono eseguite le verifiche agli SLU di Ribaltamento, Scorrimento, Carico Limite, Stabilità globale e Strutturali, applicando al muro di sostegno i carichi:
- Peso Muro
- Peso terrapieno
- Spinta Statica
- Sovraccarico e Forze esterne
ed i carichi dovuti al sisma:
- Forze di Inerzia Muro:
- Forze di Inerzia Terrapieno:
- Incremento di Spinta Sismica
Verifica a Ribaltamento
La verifica Statica per lo stato limite di ribaltamento viene effettuata secondo l’Approccio 2, con la combinazione (A1+M1+R3), tenendo conto dei valori dei coefficienti parziali riportati nelle Tabelle 6.2.I, 6.2.II e 6.5.I.
Calcolo della spinta dovuta al terreno
Il calcolo della spinta viene effettuato applicando al parametro geotecnico “angolo di attrito interno” il coefficiente gfʹ =1,00 (da Tabella 6.2.II colonna M1) , e quindi calcolando il coefficiente di spinta attiva statica Ka, utilizzando un angolo di attrito interno pari a:
fʹ = arctan(tanf /gf’)
Al parametro geotecnico “Peso dell’unità di volume” si applica il coefficiente gg =1,00 (da Tabella 6.2.II colonna M1).
Essendo il terreno, un carico permanente portato sfavorevole all’equilibrio, al valore ottenuto mediante la relazione
![]() ,
,
si applica inoltre il coefficiente parziale per l’effetto delle azioni gG =1,30 (da Tabella 6.2.I colonna A1).
Calcolo della spinta dovuta alla falda
Essendo l’acqua un carico permanente portato sfavorevole all’equilibrio, al valore ottenuto mediante la relazione
![]() ,
,
si applica il coefficiente parziale per l’effetto delle azioni gG =1,30 (da Tabella 6.2.I colonna A1).
Calcolo della spinta dovuta al sovraccarico
Essendo il sovraccarico, un carico variabile sfavorevole all’equilibrio, al valore ottenuto mediante la relazione
![]()
si applica il coefficiente parziale per l’effetto delle azioni gQ =1,5 (da Tabella 6.2.I colonna A1).
Calcolo del Momento Resistente e del Momento Ribaltante
Poichè in letteratura si riscontra che:
- le spinte possono considerarsi applicate al Paramento Interno OPPURE possono considerarsi applicate alla parete virtuale;
- la componente verticale della spinta può essere considerata come componente che diminuisce il momento ribaltante OPPURE come componente che aumenta il momento stabilizzante
il software consente di specificare il metodo di calcolo che si desidera e calcola Momento Resistente e Momento Ribaltante in funzione del metodo scelto.
|
Parametri di Calcolo - Spinte, Verifica ribaltamento e SLD |
Caso A) Sy dimnuisce il momento ribaltante
Il Momento Ribaltante è dato dalle Componenti Orizzontali delle Spinte per la distanza verticale del loro punto di applicazione rispetto al punto di rotazione O meno le Componenti Verticali per la distanza orizzontale.
Essendo le spinte dei carichi permanenti sfavorevoli alla sicurezza, alle stesse si applica il coefficiente gG1=1,3 ( da Tabella 6.2.I colonna A1)
Mrib = gG1,sfav·(Sx·dys-Sy·dxs)
Il Momento Resistente è dato dalla somma del peso proprio del muro più il peso del terreno sovrastante la mensola interna della fondazione per la distanza orizzontale tra il baricentro degli stessi ed il punto di rotazione O.
Essendo il peso proprio del muro ed il peso del terreno dei carichi permanenti a favore della sicurezza, nel calcolo del Momento Stabilizzante, agli stessi si applica il coefficiente di sicurezza gG1=1,0 ( da Tabella 6.2.I colonna A1).
Mstab = gG1,fav·(Pm·dxp+Pt·dxt)
Caso B) Sy aumenta il momento stabilizzante
Il Momento Ribaltante è dato dalle Componenti Orizzontali delle Spinte per la distanza verticale del loro punto di applicazione rispetto al punto di rotazione O.
Mrib = gG1,sfav·Sx·dys
Il Momento Resistente è dato dalla somma del peso proprio del muro più il peso del terreno sovrastante la mensola interna della fondazione per la distanza orizzontale tra il baricentro degli stessi ed il punto di rotazione O più la componente verticale delle spinte per la relativa distanza orizzontale dal punto O.
Mstab = gG1,fav·(Pm·dxp+Pt·dxt+Sy·dxs)
VERIFICA : Ed = Mrib < Rd = Mstab/gr
La verifica Sismica per lo stato limite di ribaltamento viene effettuata analogamente, secondo l’Approccio 2, con la combinazione (A1+M1+R3), ponendo pari all’unità i coefficienti parziali sulle azioni e sui parametri geotecnici (§.7.11.1) e impiegando le resistenze di progetto con i coefficienti parziali gr indicati nella tabella 7.11.III.
Considerando oltre al Peso del muro, del terrapieno e le spiinte statiche, anche le forze di inerzia e l'incremento di spinta sismica
Inoltre, si utilizzano valori di bm incrementati del 50% rispetto a quelli innanzi indicati e comunque non superiori all’unità.
Caso A) Sy dimnuisce il momento ribaltante
Mrib = Kh·(Pm·dyp+Pt·dyt) + Sx·dys-Sy·dxs + DSx·dys - DSy·dxs
Mstab = (1-Kv)·(Pm·dxp+Pt·dxt)
Caso B) Sy aumenta il momento stabilizzante
Mrib = Kh·(Pm·dyp+Pt·dyt) + Sx·dys+ DSx·dys
Mstab = (1-Kv)·(Pm·dxp+Pt·dxt) + Sy·dxs + DSy·dxs
VERIFICA : Ed = Mrib < Rd = Mstab/gr
Verifica Scorrimento
Nello stato limite ultimo di collasso per scorrimento, l’azione di progetto è data dalla componente della risultante delle forze in direzione parallela al piano di scorrimento della fondazione, mentre la resistenza di progetto è il valore della forza parallela al piano cui corrisponde lo scorrimento del muro.
Ai fini della verifica alla traslazione sul piano di posa di muri di sostegno con fondazioni superficiali, non si considera il contributo della resistenza passiva del terreno antistante il muro.
La Verifica Statica viene effettuata secondo l’Approccio 2: (A1+M1+R3) tenendo conto dei valori dei coefficienti parziali riportati nelle Tabelle 6.2.I, 6.2.II e 6.5.I.
Azione di Progetto
L’azione di Progetto Ed è data dalla somma delle forze orizzontali SFo , determinate applicando alle spinte i coefficienti di cui alla Tabella 6.2.I colonna A1, applicando ai parametri geotecnici i coefficienti di cui alla Tabella 6.2.II colonna M1.
SFo = gG1,sfav·Sx
Resistenza di Progetto
La Resistenza di Progetto Rd è data dal prodotto del coefficiente di attrito per la somma delle forze verticali f·SFv , determinate applicando alle spinte i coefficienti di cui alla Tabella 6.2.I colonna A1, applicando ai parametri geotecnici i coefficienti di cui alla Tabella 6.2.II colonna M1 ed applicando alla resistenza allo scorrimento il coefficiente di riduzione di cui alla Tabella 6.5.I colonna R3
SFv = gG1,fav·(Pm+Pt+Sy)
VERIFICA : Ed = SFo < Rd = f·SFv /gr
La Verifica Sismica viene effettuata analogamente, secondo l’Approccio 2, con la combinazione (A1+M1+R3), ponendo pari all’unità i coefficienti parziali sulle azioni e sui parametri geotecnici (§.7.11.1) e impiegando le resistenze di progetto con i coefficienti parziali gr indicati nella tabella 7.11.III.
Considerando oltre al Peso del muro, del terrapieno e le spiinte statiche, anche le forze di inerzia e l'incremento di spinta sismica
SFo = Kh·(Pm+Pt) + Sx + DSx
SFv = (1+Kv)·(Pm+Pt) + Sy + DSy
VERIFICA : Ed = SFo < Rd = f·SFv /gr
Verifica Carico Limite
Nello stato limite di collasso per raggiungimento del carico limite della fondazione, l’azione di progetto è la componente della risultante delle forze in direzione normale al piano di posa. La resistenza di progetto è il valore della forza normale al piano di posa a cui corrisponde il raggiungimento del carico limite nei terreni in fondazione.
La verifica viene condotta secondo l’Approccio 2 – Combinazione (A1+M1+R3), determinando il carico limite del complesso terreno-fondazione:
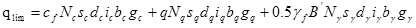
dove:
- cf = Coesione del terreno in fondazione
- Nc, Nq, Ng = fattori di portanza
- sc, sq, sg = fattori di forma
- dc, dq, dg = fattori di profondità
- ic, iq, ig = fattori di inclinazione dei carichi
- bc, bq, bg = fattori di inclinazione della base
- gc, gq, gg = fattori di inclinazione del piano di campagna
- gf = peso specifico del terreno di fondazione
- B’ = Larghezza di fondazione ridotta = Bf - 2e
- Bf = Larghezza di fondazione
- e = eccentricità dei carichi in fondazione
Azione di Progetto
L’azione di Progetto Ed è data dalla somma delle forze Verticali SFv , determinate applicando alle spinte ed ai parametri geotecnici i coefficienti di cui alle corrispondenti tabelle in relazione all’approccio utilizzato.
Resistenza di Progetto
La resistenza di progetto Rd è data dalla forza normale al piano di posa cui corrisponde il carico limite applicando il coefficiente gR di cui alla tabella 6.5.I in relazione all’approccio utilizzato.
Rd = qlim Bʹ / γR
VERIFICA Ed < Rd
Verifica Stabilità Globale
La verifica di stabilità globale viene effettuata secondo l'Approccio 1 Combinazione 2 (A2+M2+R2) tenendo conto dei coefficienti parziali riportati nelle Tabelle 6.2.I e 6.2.II per le azioni e i parametri geotecnici, e nella Tab. 6.8.I per le resistenze globali.
Con riferimento a quanto riportato nella Circolare 21/01/2019 N. 7 all’art. C6.5.3.1.1 per la verifica di stabilità globale del complesso opera di sostegno-terreno, si rimanda alla sezione relativa alle opere di materiali sciolti e ai fronti di scavo.
Nel software, viene utilizzato il metodo di Bishop o metodo delle strisce.
Dopo avere scelto e disegnato una o più sezioni longitudinali del pendio in base alla massima pendenza e/o ad altre condizioni critiche come la presenza di strutture o infrastrutture, di discontinuità morfologiche o geologiche, si ipotizza una superficie cilindrica di scorrimento potenziale, S, e si suddivide idealmente la porzione di terreno delimitato da S e dalla superficie topografica in n conci mediante n-1 tagli verticali tali che l’arco di cerchio alla base di ciascuno di essi ricada interamente in un unico tipo di terreno.
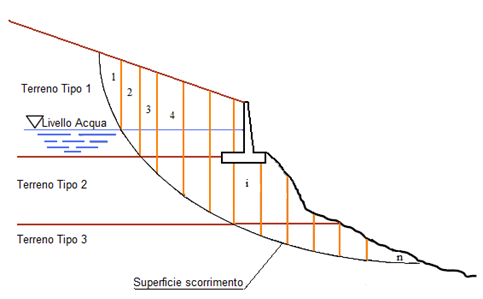
|
Analizzando il singolo concio i-esimo, e considerando le hp. semplificative del metodo di Bishop:
le forze agenti sul concio sono:
|
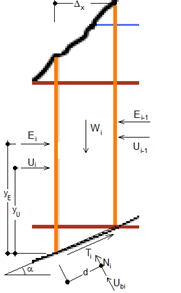 |
Dalle equazioni di equilibrio alla traslazione verticale ed orizzontale:
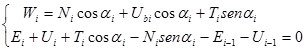
Si ricava:
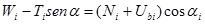
ed essendo:
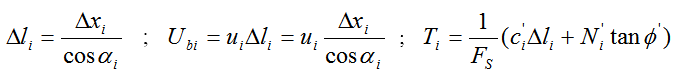
si ha:
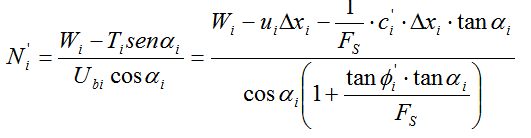
E quindi:
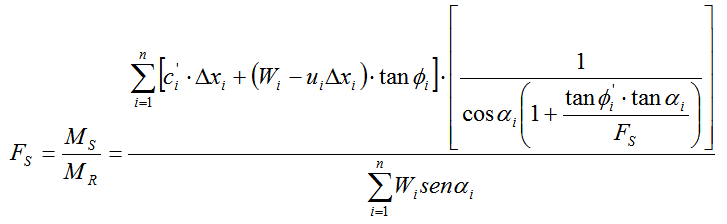
La soluzione è ricercata per via iterativa fissando un primo valore di tentativo per FS.
Il coefficiente di sicurezza calcolato è relativo alla superficie di scorrimento potenziale considerata. Il valore minimo di FS corrisponde alla superficie di scorrimento potenziale critica e deve essere determinato per tentativi.
A titolo indicativo, se la conoscenza delle condizioni stratigrafiche e geotecniche è buona, e le conseguenze di una eventuale rottura non sono particolarmente drammatiche, per le verifiche di stabilità di scavi o di pendii naturali “a priori”, ovvero se non si è manifestata la frana, si può adottare un coefficiente di sicurezza compreso tra 1,3 e 1,4 in relazione al metodo di calcolo impiegato, mentre per le verifiche di stabilità “a posteriori”, ovvero dopo che si è manifestata la frana, e quindi si conosce la superficie di scorrimento e si utilizza la resistenza al taglio residua del terreno, potranno essere adottati coefficienti di sicurezza minimi compresi tra 1,2 e 1,3.
Verifiche Strutturali
Le verifiche di resistenza vengono effettuate secondo l’Approccio 2: (A1+M1+R3).
Muri in c.a.
Sul paramento si effettua il calcolo delle armature e la verifica allo SLU di presso-flessione e taglio in corrispondenza delle sezioni
- - di attacco tra il paramento e la fondazione (quota 0.00m)
- - posta ad Hm/3
- - posta a 2·Hm/3.
Inoltre, si effettua il calcolo delle armature e la relativa verifica allo SLU di flessione e taglio della fondazione, considerando la mensola esterna soggetta alle tensioni trasmesse dal terreno sottostante e la mensola interna soggetta alle tensioni del terreno ed al peso del terreno sovrastante.
A tal fine, si riporta in appresso, quanto indicato dalla normativa vigente per le Resistenze dei Materiali, per le resistenze strutturali e per le necessarie verifiche di Resistenza da effettuare, implementato nel software in oggetto.
In accordo con il Cap. 11, le resistenze di progetto fd indicano le resistenze dei materiali, calcestruzzo ed acciaio, ottenute mediante l’espressione:
fd = fk / gM
dove:
- fk sono le resistenze caratteristiche del materiale;
- gM sono i coefficienti parziali per le resistenze, comprensivi delle incertezze del modello e della geometria, che possono variare in funzione del materiale, della situazione di progetto e della particolare verifica in esame.
Per il calcestruzzo la resistenza di calcolo a compressione, fcd , é:
fcd = acc·fck / gc (4.1.3)
dove:
- acc è il coefficiente riduttivo per le resistenze di lunga durata;
- gc è il coefficiente parziale di sicurezza relativo al calcestruzzo;
- fck è la resistenza caratteristica cilindrica a compressione del calcestruzzo a 28 giorni.
Il coefficiente gc è pari ad 1,5; Il coefficiente acc è pari a 0,85.
La resistenza di calcolo a trazione, fctd , vale:
fctd = fctk / gc (4.1.4)
dove:
- gc è il coefficiente parziale di sicurezza relativo al calcestruzzo già definito al § 4.1.2.1.1.1;
- fctk è la resistenza caratteristica a trazione del calcestruzzo (§ 11.2.10.2).
La resistenza di calcolo dell’acciaio fyd è riferita alla tensione di snervamento ed il suo valore è dato da:
fyd = fyk / gs (4.1.5)
dove:
- gs è il coefficiente parziale di sicurezza relativo all’acciaio, pari a 1,15;
- fyk per armatura ordinaria è la tensione caratteristica di snervamento dell’acciaio (v. § 11.3.2).
La resistenza tangenziale di aderenza di calcolo fbd vale:
fbd = fbk / gc (4.1.6)
dove:
- gc è il coefficiente parziale di sicurezza relativo al calcestruzzo, pari a 1,5;
- fbk è la resistenza tangenziale caratteristica di aderenza data da:
- fbk = 2,25×h1×h2× fctk (4.1.7)
in cui
- h1 = 1,0 in condizioni di buona aderenza
- h1 = 0,7 in condizioni di non buona aderenza, quali nei casi di armature molto addensate, ancoraggi in zona tesa, ancoraggi in zone superiori di getto, in elementi strutturali realizzati con casseforme scorrevoli
- h2 = 1,0 per barre di diametro f < 32 mm
- h2 = (132 - f)/100 per barre di diametro superiore.
La lunghezza di ancoraggio di progetto e la lunghezza di sovrapposizione sono influenzate dalla forma delle barre, dal copriferro, dall'effetto di confinamento dell'armatura trasversale, dalla presenza di barre trasversali saldate, dalla pressione trasversale lungo la lunghezza di ancoraggio e dalla percentuale di armatura sovrapposta rispetto all'armatura totale. Per le regole di dettaglio da adottare si potrà fare utile riferimento alla sezione 8 di UNI EN 1992-1-1:2015
Verifica Pressoflessione
Con riferimento alla sezione pressoinflessa, rappresentata in Figura, la capacità, in termini di resistenza e duttilità, si determina in base alle ipotesi di calcolo e ai modelli s-e.
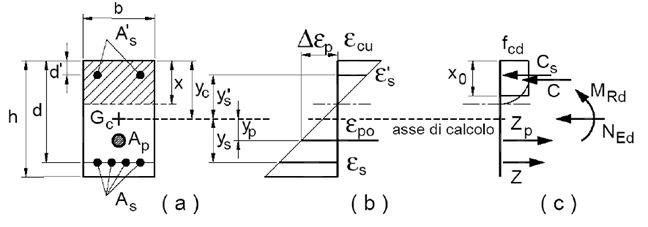
Sezione pressoinflessa
assieme ai diagrammi di deformazione e di sforzo così come dedotti dalle ipotesi e dai modelli s-e di cui nei punti precedenti, la verifica di resistenza (SLU) si esegue controllando che:
MRd = MRd(NEd) ≥ MEd (4.1.18a)
dove
- MRd è il valore di progetto del momento resistente corrispondente a NEd;
- NEd è il valore di progetto della componente assiale (sforzo normale) dell’azione;
- MEd è il valore di progetto della componente flettente dell’azione.
Verifica a Taglio
La verifica di resistenza (SLU) si pone con
VRd ≥ VEd (4.1.22)
dove
VEd è il valore di progetto dello sforzo di taglio agente.
VRd è la resistenza di progetto
VRd = min (VRsd, VRcd)
Verifiche Stati Limite di Esercizio
Nei muri in c.a. viene eseguita la Verifica dello stato limite di apertura delle fessure, nel quale il valore limite di apertura della fessura calcolato al livello considerato è pari ad uno dei seguenti valori nominali:
w1 = 0,2 mm w2 = 0,3 mm w3 = 0,4 mm
Lo stato limite di fessurazione deve essere fissato in funzione delle condizioni ambientali e della sensibilità delle armature alla corrosione, come descritto nel seguito.
Condizioni ambientali ( § 4.1.2.2.4.2)
Ai fini della protezione contro la corrosione delle armature metalliche e della protezione contro il degrado del calcestruzzo, le condizioni ambientali possono essere suddivise in ordinarie, aggressive e molto aggressive in relazione a quanto indicato nella Tab. 4.1.III con riferimento alle classi di esposizione definite nelle Linee Guida per il calcestruzzo strutturale emesse dal Servizio Tecnico Centrale del Consiglio Superiore dei Lavori Pubblici nonché nella UNI EN 206:2016.

Sensibilità delle armature alla corrosione ( § 4.1.2.2.4.3)
Le armature si distinguono in due gruppi:
- – armature sensibili;
- – armature poco sensibili.
Appartengono al primo gruppo gli acciai da precompresso, appartengono al secondo gruppo gli acciai ordinari.
Per gli acciai zincati e per quelli inossidabili, si può tener conto della loro minor sensibilità alla corrosione sulla base di documenti di comprovata validità.
Scelta degli stati limite di fessurazione ( § 4.1.2.2.4.4)
Nella Tab. 4.1.IV sono indicati i criteri di scelta dello stato limite di fessurazione con riferimento alle esigenze sopra riportate.
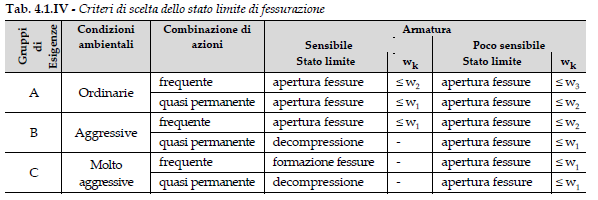
w1, w2, w3 sono definiti al § 4.1.2.2.4, il valore wk è definito al § 4.1.2.2.4.5.
Verifica dello stato limite di fessurazione (art. 4.1.2.2.4.5)
Stato limite di decompressione e di formazione delle fessure
Le tensioni sono calcolate in base alle caratteristiche geometriche e meccaniche della sezione omogeneizzata non fessurata.
Stato limite di apertura delle fessure
Il valore caratteristico di apertura delle fessure (wk) non deve superare i valori nominali w1, w2, w3 secondo quanto riportato nella Tab. 4.1.IV.
L’ampiezza caratteristica delle fessure wk è calcolata come 1,7 volte il prodotto della deformazione media delle barre d’armatura esm per la distanza media tra le fessure Dsm:
wk = 1,7 esm·Dsm (4.1.14)
Per il calcolo di esm e Dsm vanno utilizzati criteri consolidati riportati in documenti di comprovata validità.
La verifica dell’ampiezza di fessurazione può anche essere condotta senza calcolo diretto, limitando la tensione di trazione nell’armatura, valutata nella sezione parzializzata per la combinazione di carico pertinente, ad un massimo correlato al diametro delle barre ed alla loro spaziatura.
Come indicato al punto C.4.1.2.2.4 della Circolare 21 gennaio 2019 n.7 C.S.LL.PP., “Istruzioni per l’applicazione dell’Aggiornamento delle «Norme tecniche per le costruzioni» di cui al decreto ministeriale 17 gennaio 2018.”:
la deformazione unitaria media delle barre esm può essere calcolata con l’espressione:
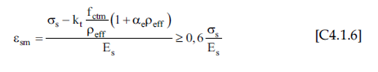
in cui:
- ss è la tensione nell’armatura tesa considerando la sezione fessurata;
- ac è il rapporto Es/Ecm;
- reff è pari a As/Ac,eff
- Ac,eff è l’area efficace di calcestruzzo teso attorno all’armatura, di altezza hc,ef,
- hc,ef è il valore minore tra 2,5(h-d), (h-x)/3. o h/2
- nel caso di elementi in trazione, in cui esistono due aree efficaci, l’una all’estradosso e l’altra all’intradosso, entrambe le aree vanno considerate separatamente;
- kt è un fattore dipendente dalla durata del carico e vale:
- kt = 0,6 per carichi di breve durata,
- kt = 0,4 per carichi di lunga durata.
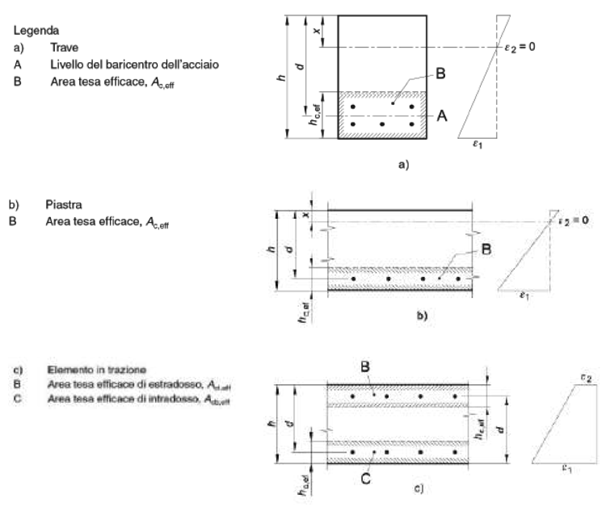
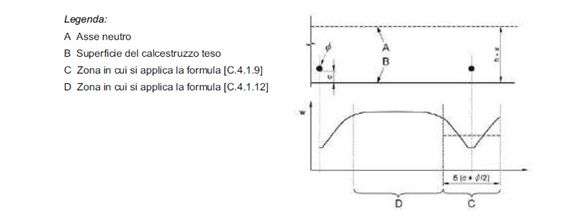
Nei casi in cui l’armatura sia disposta con una spaziatura non superiore a 5(c + f/2) (vedi Figura C4.1.11), la distanza media tra le fessure, Dsm, può essere valutata con l’espressione:
![]()
in cui:
- f è il diametro delle barre. Se nella sezione considerata sono impiegate barre di diametro diverso, si
- raccomanda di adottare un opportuno diametro equivalente feq.
- c è il ricoprimento dell’armatura;
- k1 = 0,8 per barre ad aderenza migliorata,
- = 1,6 per barre lisce;
- k2 = 0,5 nel caso di flessione,
- = 1,0 nel caso di trazione semplice.
- k3 = 3,4
- k4 = 0,425.
Nelle zone in cui l’armatura è disposta con una spaziatura superiore a 5(c + f/2) Vedi figura seguente, per la parte di estensione 5(c + f/2) nell’intorno delle barre la distanza media tra le fessure, Dsm, può essere valutata ancora con l’espressione C4.1.7.
Nella parte rimanente la distanza media tra le fessure, Dsm, può, invece, essere valutata con l’espressione:
Dsm = 0,75(h-x)
in cui:
(h – x) è la distanza tra l’asse neutro ed il lembo teso della membratura.
Verifica Stato Limite di Danno
La verifica allo Stato Limite di Danno viene eseguita, nel rispetto di quanto indicato al §.7.11.6.2.2 del DM.2018, verificando che gli spostamenti permanenti indotti dal sisma siano compatibili con la funzionalità dell’opera e con quella di eventuali strutture o infrastrutture interagenti con essa.
I criteri di scelta dei valori limite di spostamento (Dmax) devono essere illustrati e giustificati dal progettista.
Detto D lo spostamento indotto dal sisma, lo stesso può essere determinato mediante la formula di Richards & Elms:
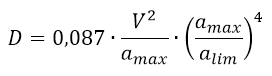
dove:
- V = 0,16 · amax·g·SS·ST
- amax = accelerazione sismica adimensionale SLD
- g = 9,80665 = accelerazione di gravità
- SS = coefficiente di amplificazione stratigrafico
- ST = coefficiente di amplificazione topografico
- alim = accelerazione oltre la quale si innesca lo scorrimento della fondazione per superamento del limite dell'attrito
|
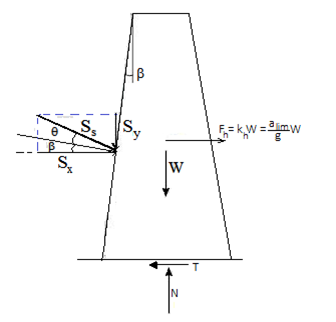
Per il calcolo di alim si osservi che, considerando tutte le forze agenti sul muro, per l’equilibrio alla traslazione orizzontale e verticale deve aversi:
Imponendo che risulti T = N·tg(qf) si ricava:
da cui: |
 |
Si osservi che, con il metodo di Richards e Elms la Spinta S viene calcolata con la teoria di Mononobe-Okabe, trascurando l’accelerazione verticale e sostituendo al posto del coefficiente sismico orizzontale kh il coefficiente sismico orizzontale limite kh = alim /g.
Per determinare alim con a formula sopra scritta, risulta pertanto necessaria una procedura iterativa, poiché la spinta del terreno S dipende in modo non lineare da kh.
-
Alim = 0.01: AlimC=0
While Alim<>AlimC
AlimC=Alim
Kh = Alim / 9.81
Kv = 0.5 * Kh
S = SpintaSismica
Sx = SS*Cos(q+b)
Sy = SS*Sin(q+b)
Alim = (Tan(qf) + (Sy* Tan(qf) - Sx) / W) * 9.81
Wend
D = 0.087 * (V ^ 2 / AmaxSLD) * (AmaxSLD / Alim) ^ 4
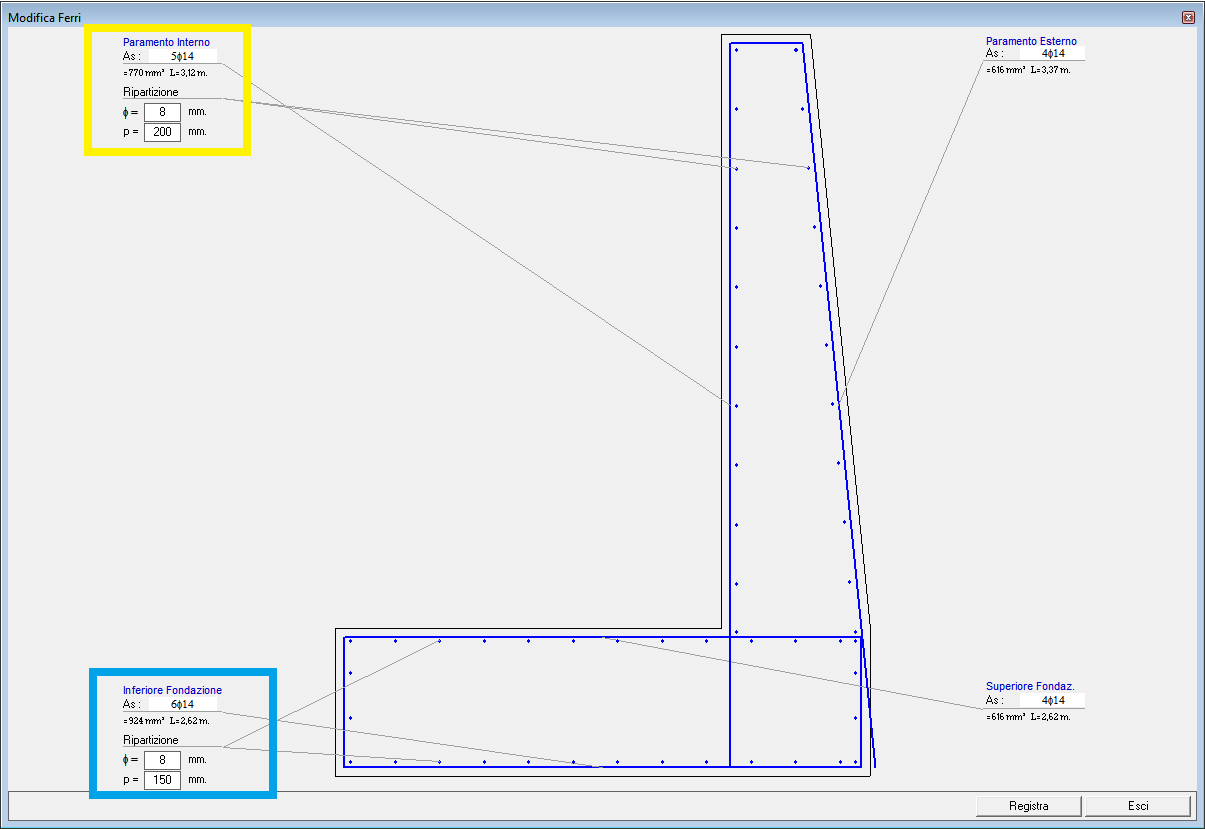
Modifica Armature
L'opzione "Verifica – Modifica Armature" attiva solo nel caso di muri in cemento armato, apre una finestra di dialogo che consente all’utente di modificare i ferri determinati dal programma.
|
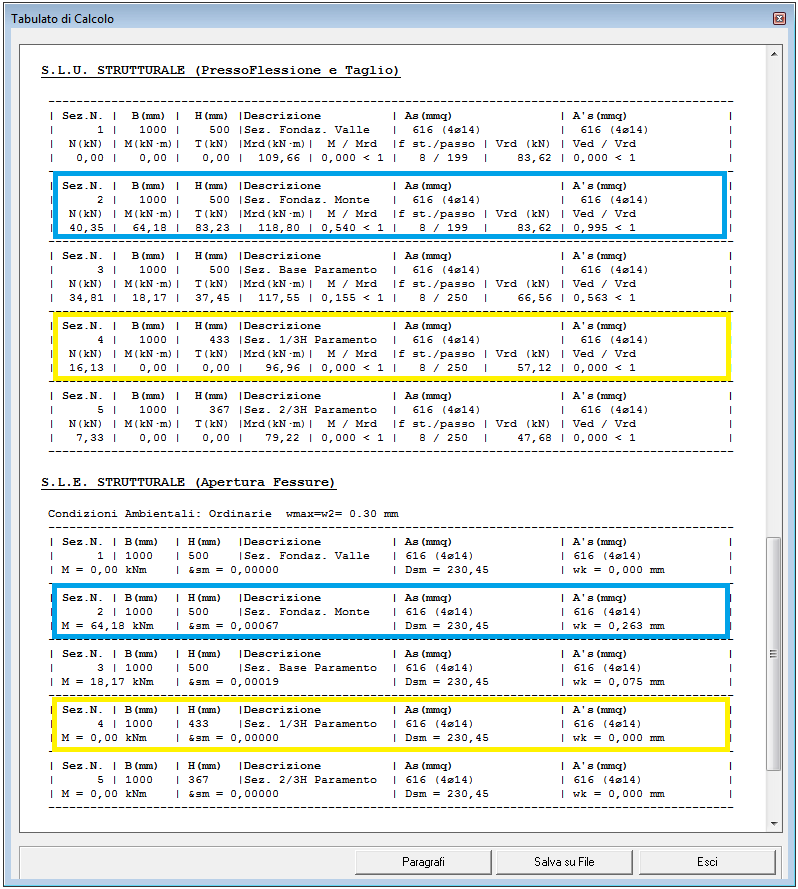
Armature determinate dal software |
|
Armature Modificate dall'Utente |
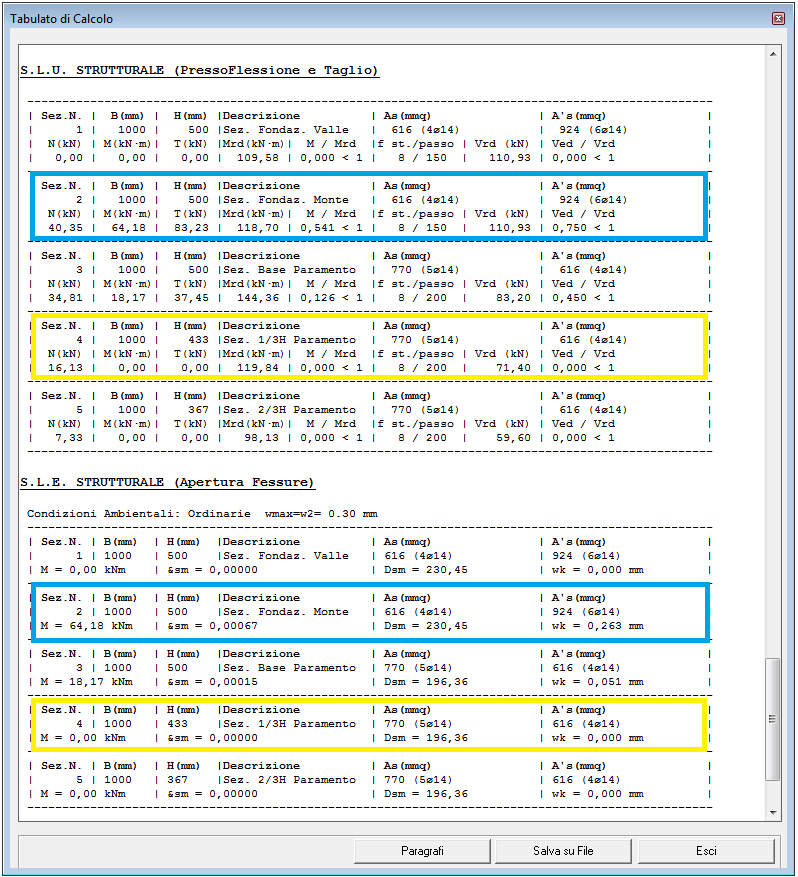
Specificate le nuove armature, desiderate dall’utente, e selezionando il pulsante registra, il programma riavvia immediatamente la verifica e mostra i relativi risultati:
|
Risultati Verifiche - Armature inserite dall'utente |
Relazioni
Il comando “genera” consente di attivare il menu a discesa da cui è possibile selezionare i sottocomandi per creare i seguenti documenti:
- Tabulato di Calcolo;
- Relazione di Calcolo;
- Relazione sui Materiali;
- Relazione Geotecnica;
- Relazione sulle Fondazioni;
- Piano di Manutenzione;
- Esecutivi di Cantiere;
- Computo Materiali.
Tabulato di Calcolo
Selezionando tale comando, si attiva una finestra di dialogo in cui è possibile selezionare il contenuto della relazione,
|
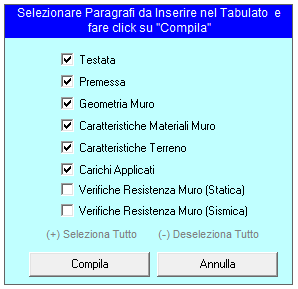 |
Ad es. nel caso in cui desidera solo la stampa della geometria del muro bisogna attivare solo l’opzione 3.
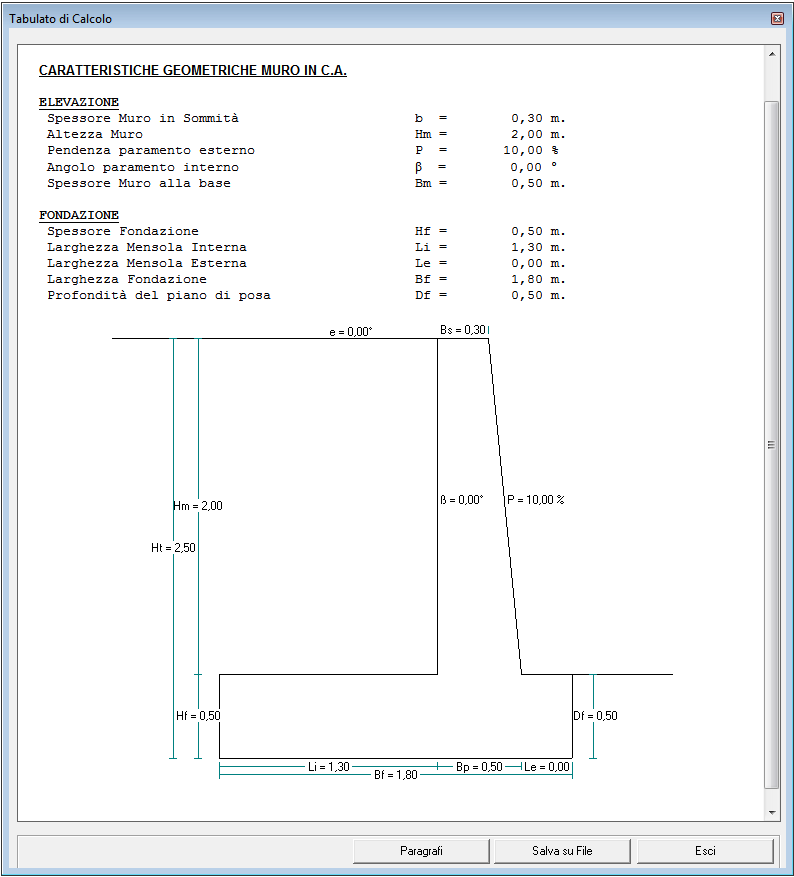
Selezionando il comando “Compila” verrà mostrata a video l’anteprima della relazione, con evidenziate eventuali verifiche non soddisfatte.
|
Caratteristiche Geometriche Muro |
Selezionando il comando “Salva su File” verrà chiesto il nome del file (formato Word) in cui salvare il documento.
Crea File Word - Tabulato di Calcolo
Relazione di Calcolo
Selezionando tale comando, viene richiesto il nome del file da creare,
Crea File Word - Relazione di Calcolo
quindi viene generata una relazione, contenente:
- una premessa con i dati del calcolo, del committente, etc.
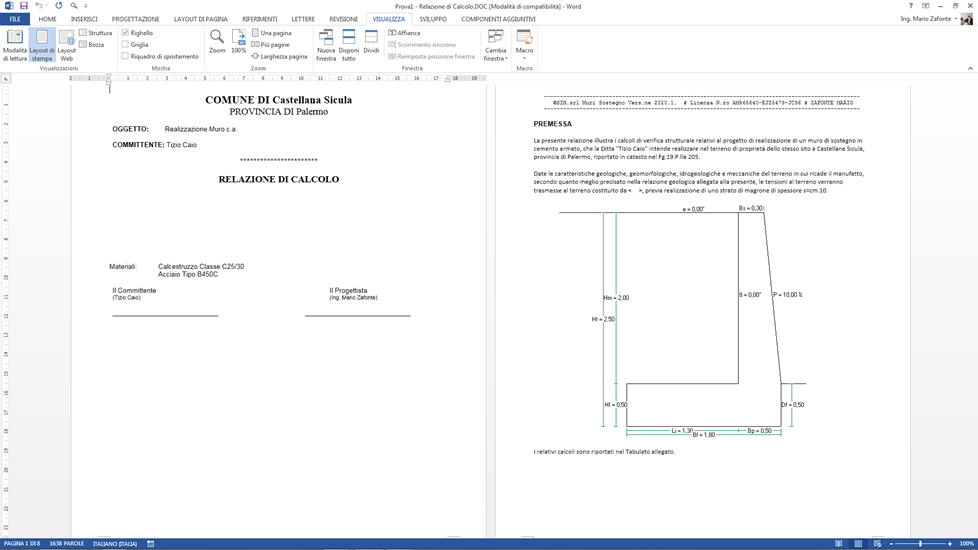
- la normativa di riferimento, i materiali utilizzati
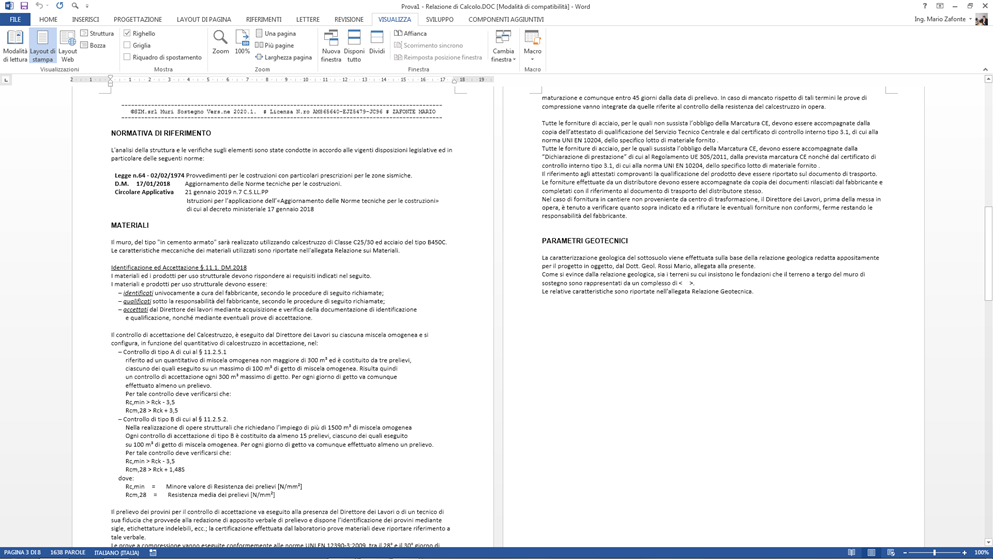
- i metodi di verifica
Tale relazione può ovviamente essere modificata e personalizzata a scelta dell’utente.
Esecutivi di Cantiere
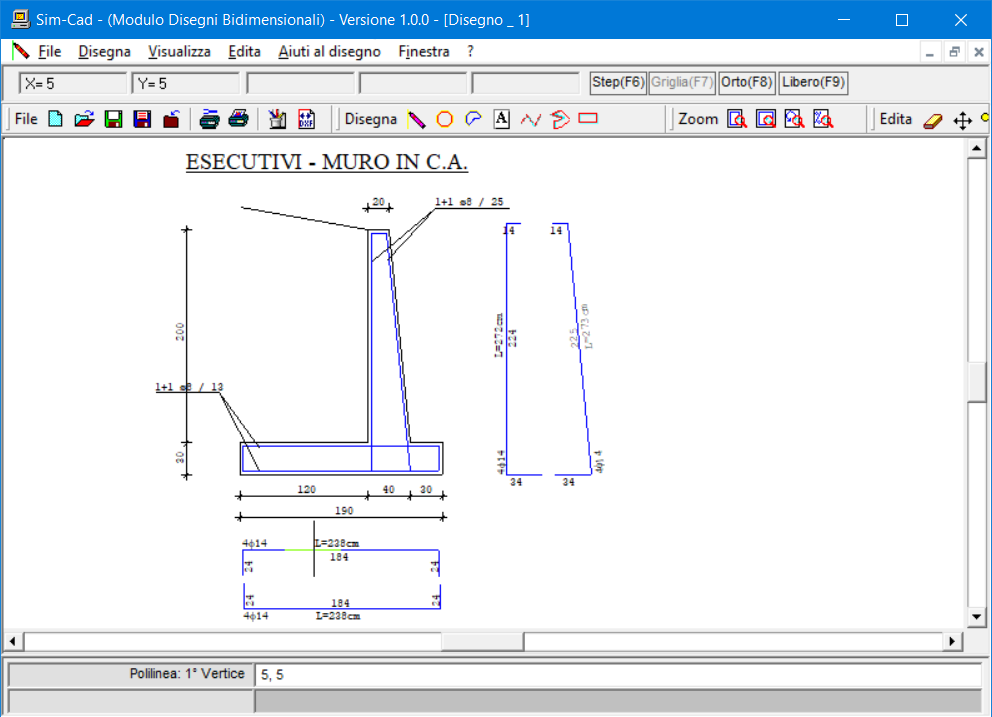
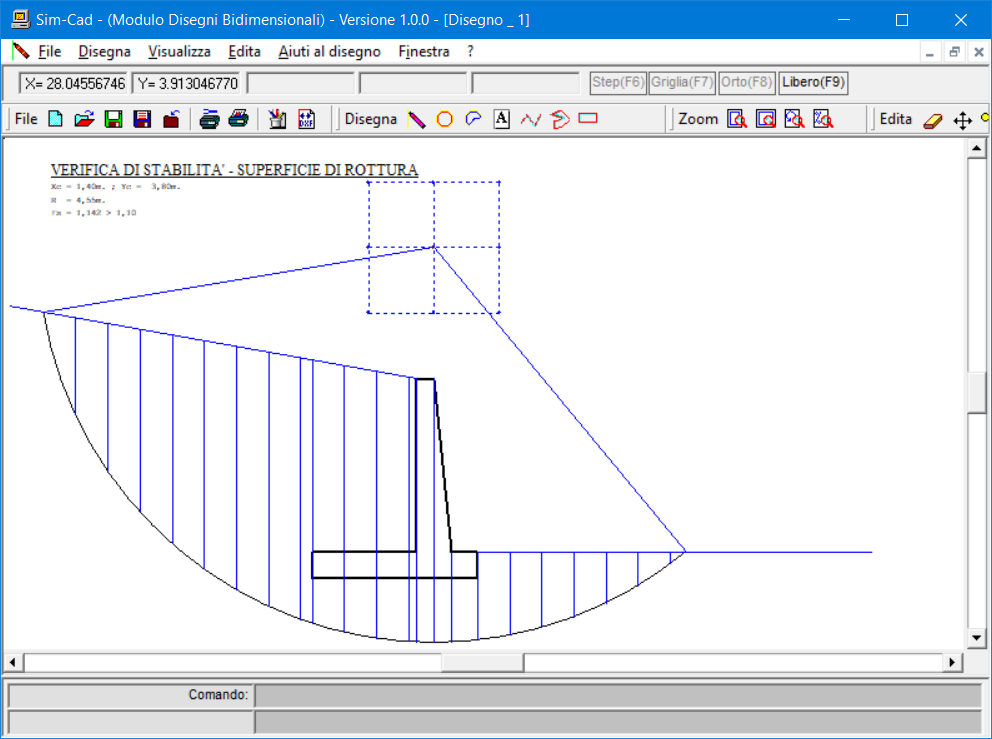
Il comando “Genera” -> “Esecutivi di Cantiere” consente di disegnare il muro, con le relative armature e la superficie di rottura relativa alla verifica di stabilità globale.
Tali disegni verranno generati tramite il programma SIM-CAD (che nella versione 1 è distribuito gratuitamente).
|
Esecutivi di Cantiere - Distinta Armature
Superficie di Rottura |
Mediante il SIM-CAD è possibile effettuare modifiche al disegno creato, aggiungere testo, linee, ecc., stampare, creare un immagine BMP dello stesso, creare un file DXF, ecc.
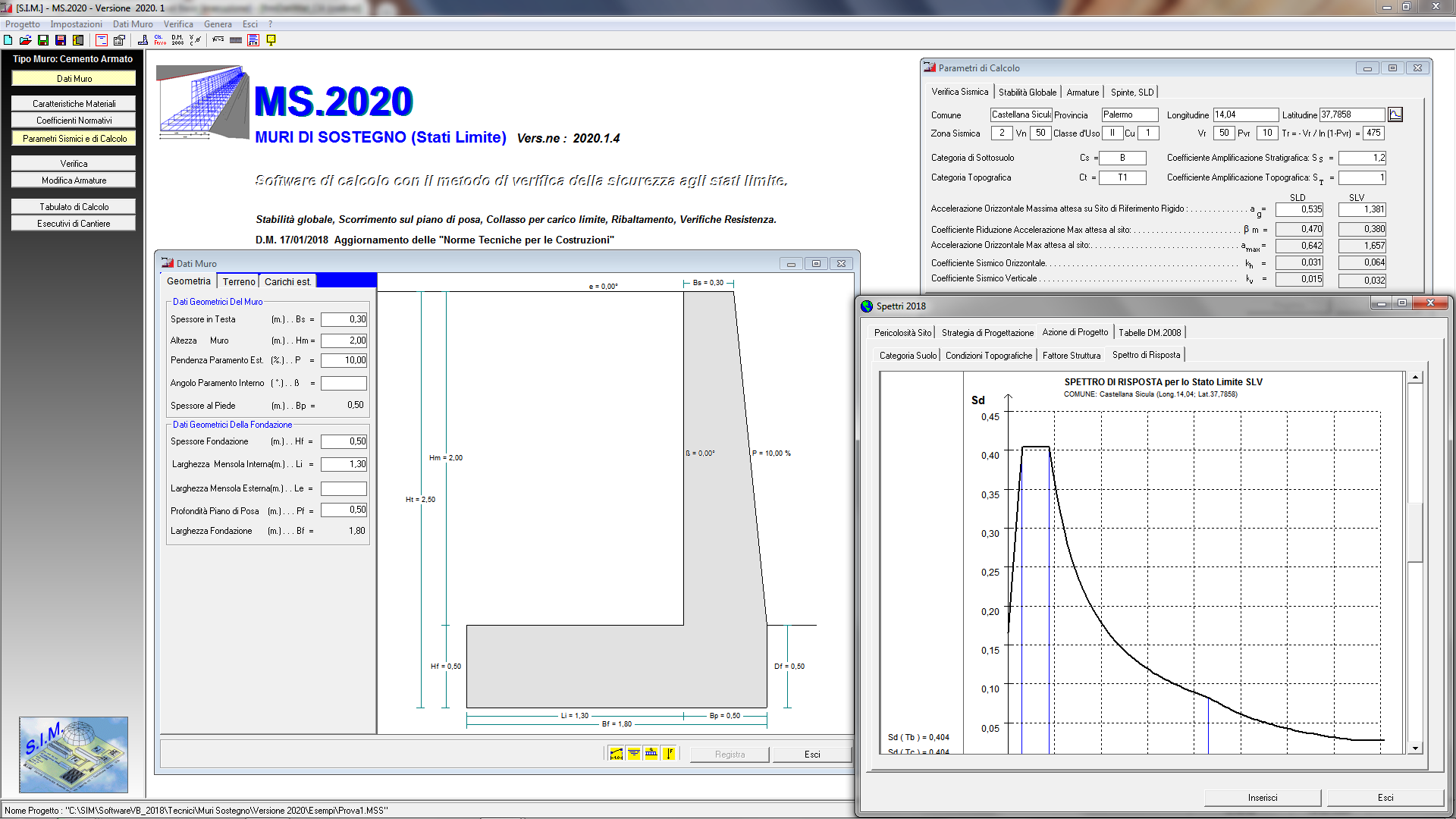

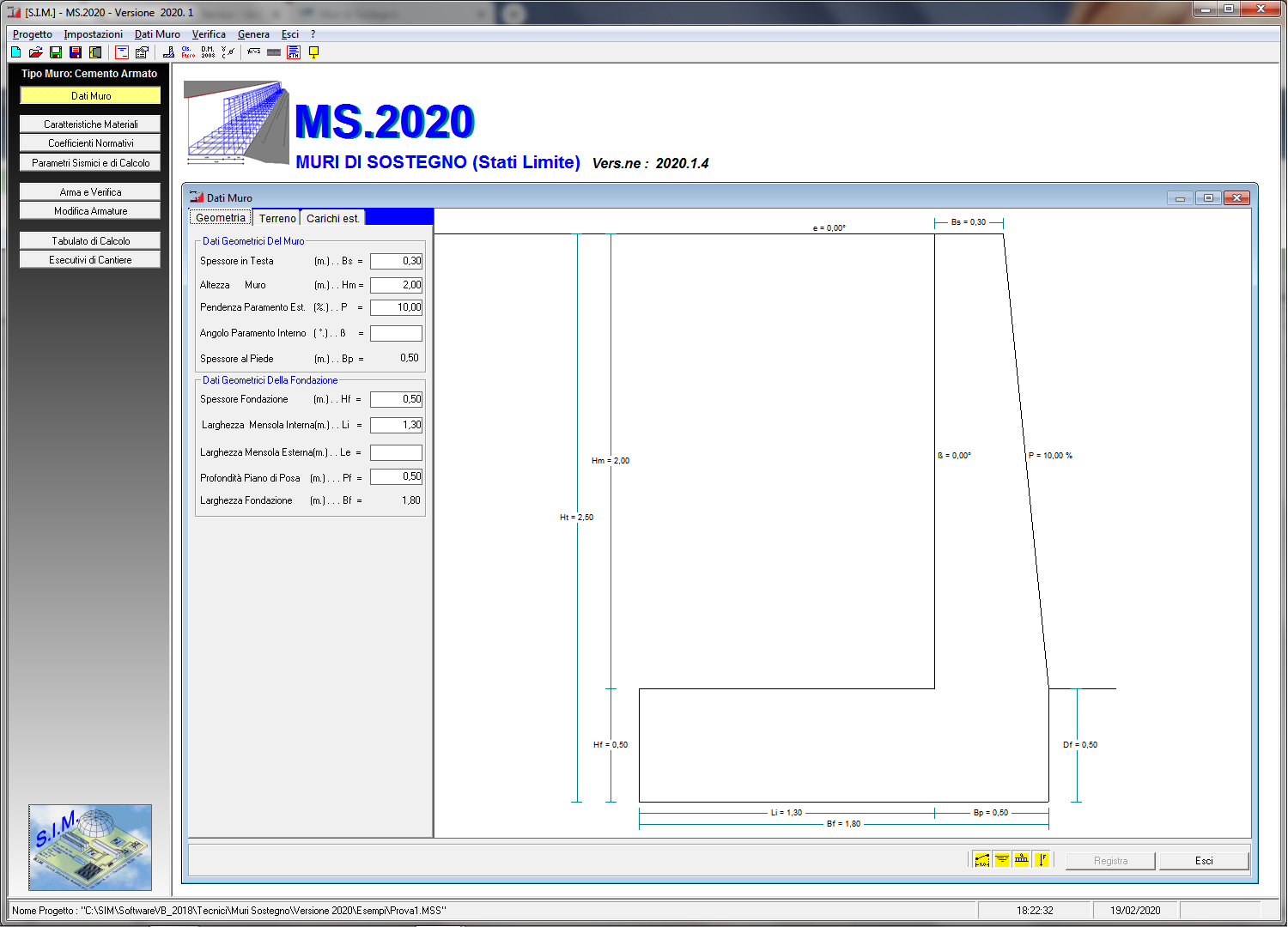
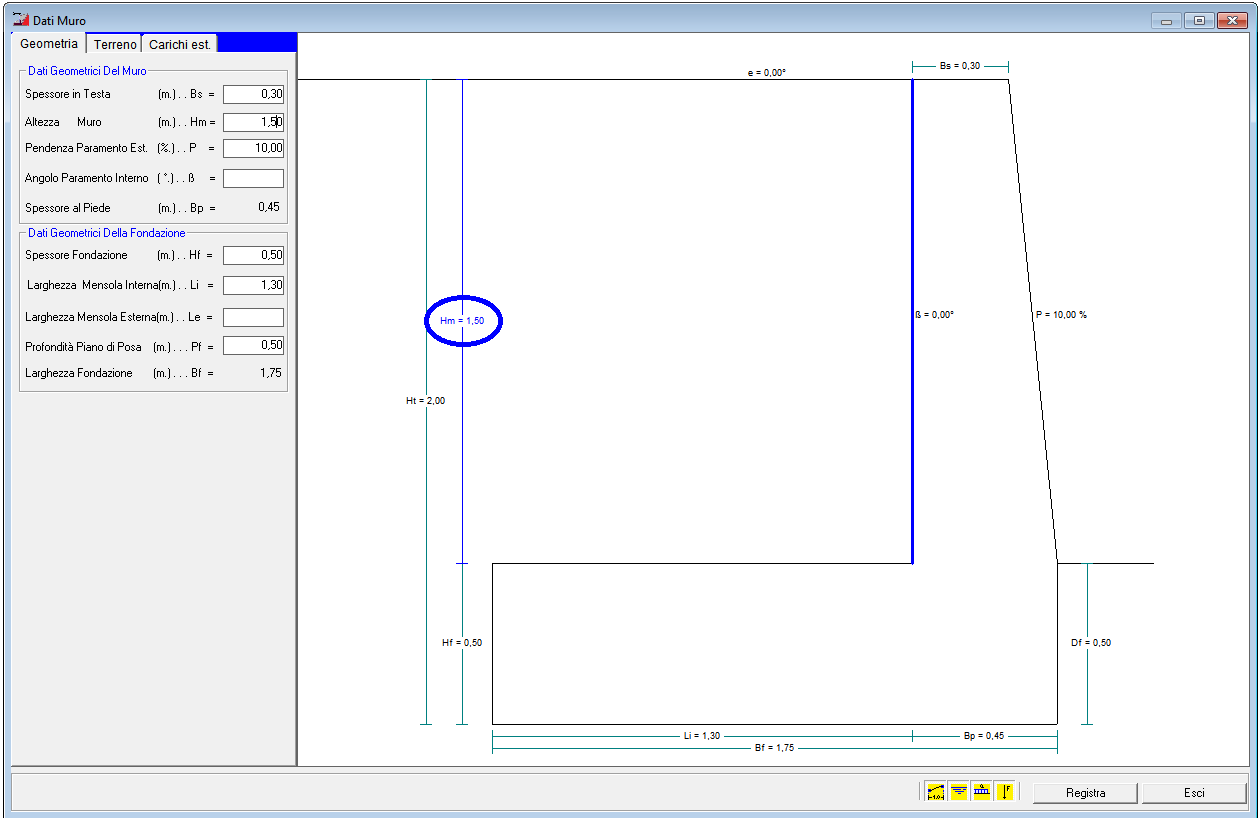 Geometria Muro
Geometria Muro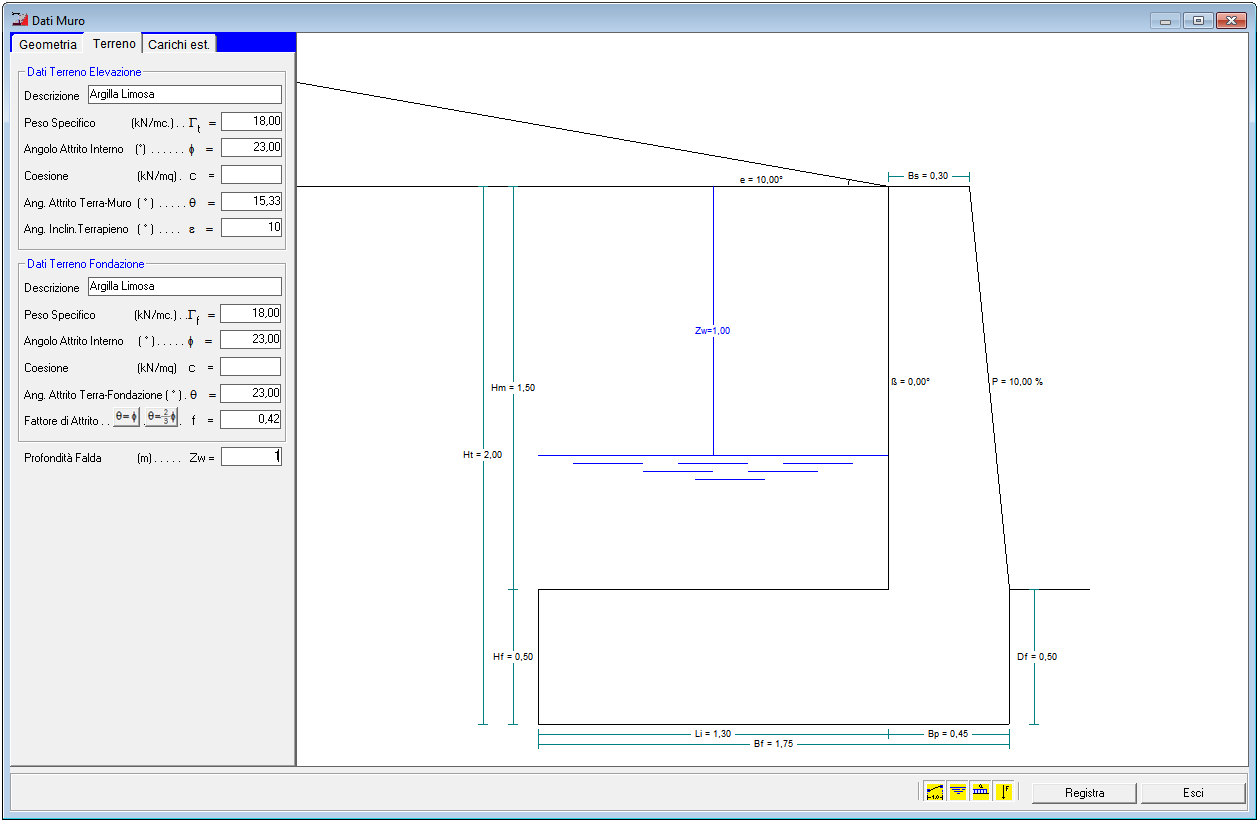 Caratteristiche Geotecniche Terreno
Caratteristiche Geotecniche Terreno 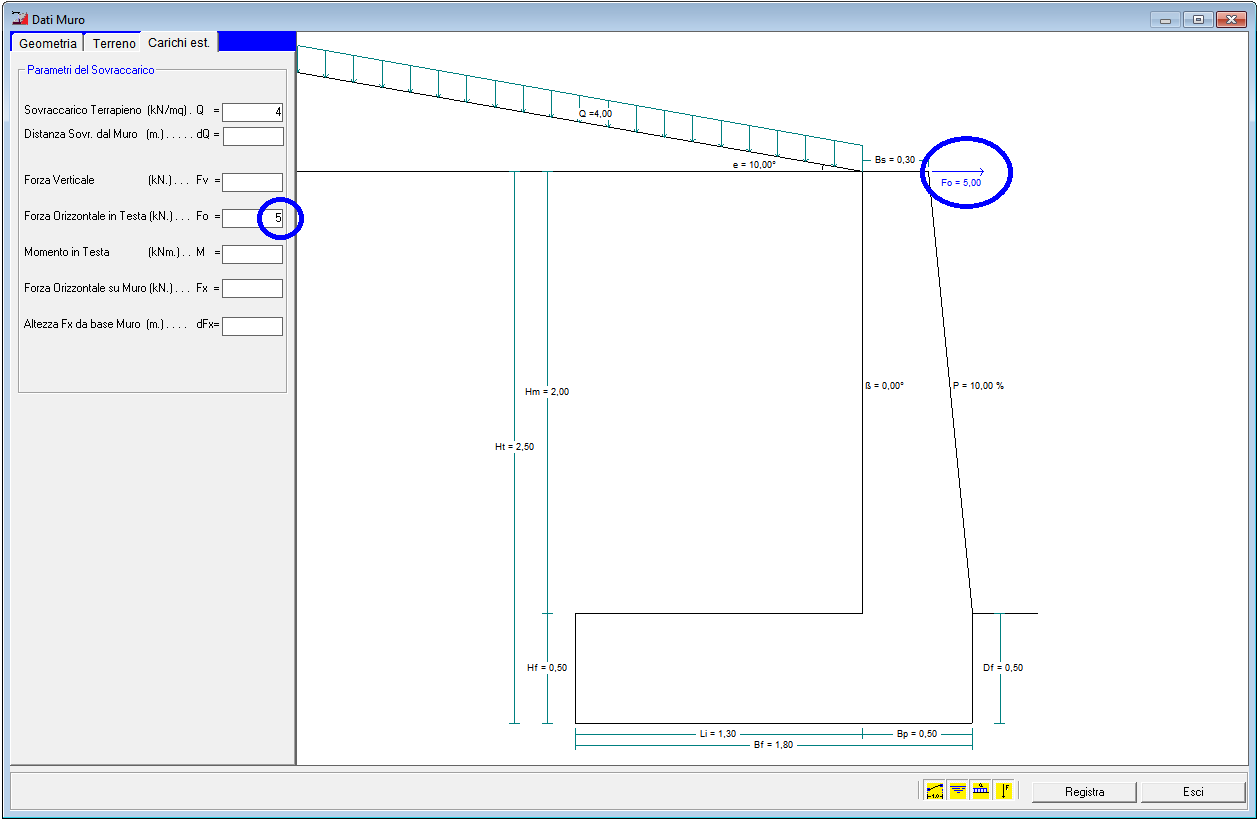
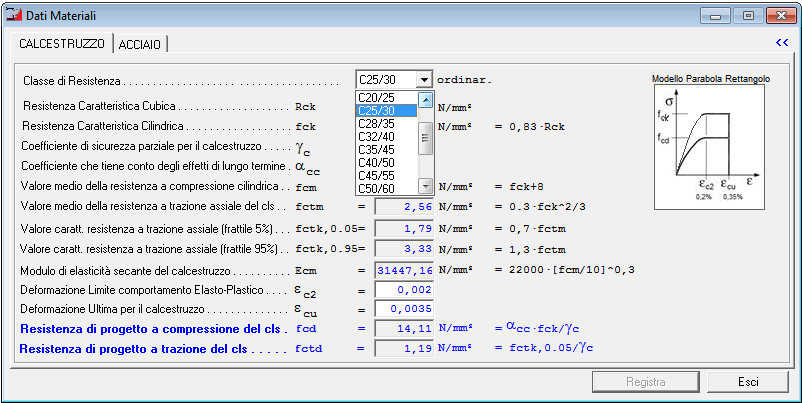
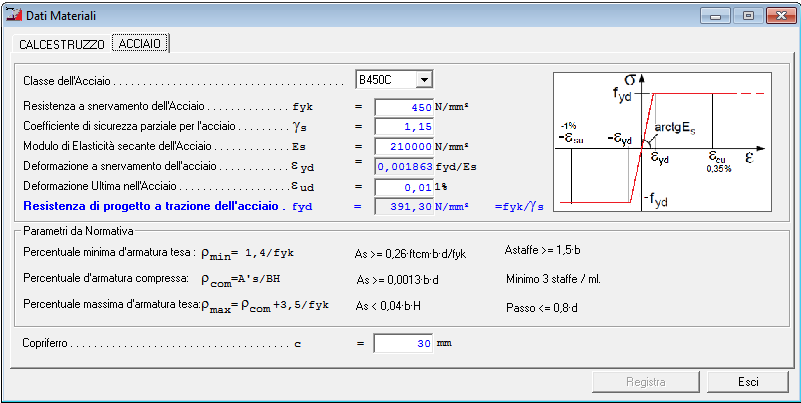
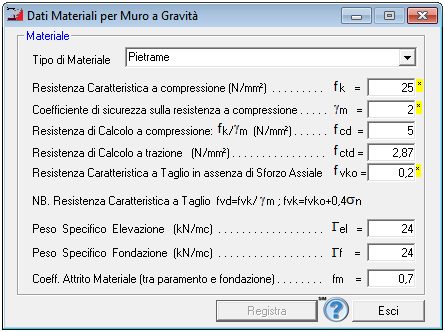
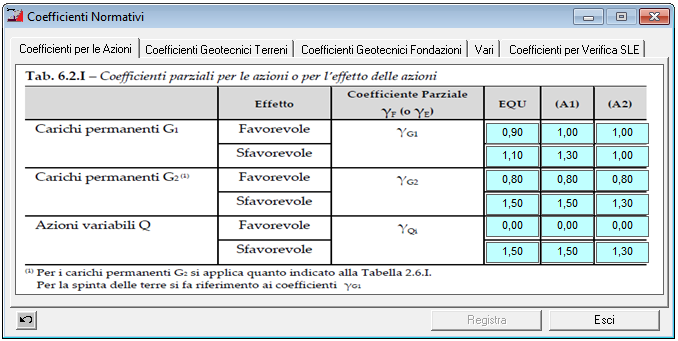 Tabella 6.2.I – Coefficienti per le Azioni
Tabella 6.2.I – Coefficienti per le Azioni