Verifica a Ribaltamento
La verifica Statica per lo stato limite di ribaltamento viene effettuata secondo l’Approccio 2, con la combinazione (A1+M1+R3), tenendo conto dei valori dei coefficienti parziali riportati nelle Tabelle 6.2.I, 6.2.II e 6.5.I.
Calcolo della spinta dovuta al terreno
Il calcolo della spinta viene effettuato applicando al parametro geotecnico “angolo di attrito interno” il coefficiente gfʹ =1,00 (da Tabella 6.2.II colonna M1) , e quindi calcolando il coefficiente di spinta attiva statica Ka, utilizzando un angolo di attrito interno pari a:
fʹ = arctan(tanf /gf’)
Al parametro geotecnico “Peso dell’unità di volume” si applica il coefficiente gg =1,00 (da Tabella 6.2.II colonna M1).
Essendo il terreno, un carico permanente portato sfavorevole all’equilibrio, al valore ottenuto mediante la relazione
![]() ,
,
si applica inoltre il coefficiente parziale per l’effetto delle azioni gG =1,30 (da Tabella 6.2.I colonna A1).
Calcolo della spinta dovuta alla falda
Essendo l’acqua un carico permanente portato sfavorevole all’equilibrio, al valore ottenuto mediante la relazione
![]() ,
,
si applica il coefficiente parziale per l’effetto delle azioni gG =1,30 (da Tabella 6.2.I colonna A1).
Calcolo della spinta dovuta al sovraccarico
Essendo il sovraccarico, un carico variabile sfavorevole all’equilibrio, al valore ottenuto mediante la relazione
![]()
si applica il coefficiente parziale per l’effetto delle azioni gQ =1,5 (da Tabella 6.2.I colonna A1).
Calcolo del Momento Resistente e del Momento Ribaltante
Poichè in letteratura si riscontra che:
- le spinte possono considerarsi applicate al Paramento Interno OPPURE possono considerarsi applicate alla parete virtuale;
- la componente verticale della spinta può essere considerata come componente che diminuisce il momento ribaltante OPPURE come componente che aumenta il momento stabilizzante
il software consente di specificare il metodo di calcolo che si desidera e calcola Momento Resistente e Momento Ribaltante in funzione del metodo scelto.
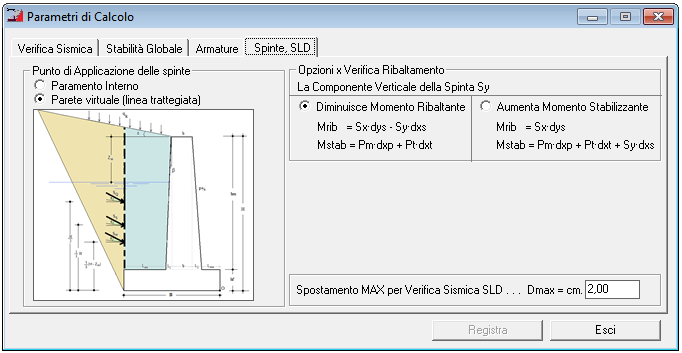
|
Parametri di Calcolo - Spinte, Verifica ribaltamento e SLD |
Caso A) Sy dimnuisce il momento ribaltante
Il Momento Ribaltante è dato dalle Componenti Orizzontali delle Spinte per la distanza verticale del loro punto di applicazione rispetto al punto di rotazione O meno le Componenti Verticali per la distanza orizzontale.
Essendo le spinte dei carichi permanenti sfavorevoli alla sicurezza, alle stesse si applica il coefficiente gG1=1,3 ( da Tabella 6.2.I colonna A1)
Mrib = gG1,sfav·(Sx·dys-Sy·dxs)
Il Momento Resistente è dato dalla somma del peso proprio del muro più il peso del terreno sovrastante la mensola interna della fondazione per la distanza orizzontale tra il baricentro degli stessi ed il punto di rotazione O.
Essendo il peso proprio del muro ed il peso del terreno dei carichi permanenti a favore della sicurezza, nel calcolo del Momento Stabilizzante, agli stessi si applica il coefficiente di sicurezza gG1=1,0 ( da Tabella 6.2.I colonna A1).
Mstab = gG1,fav·(Pm·dxp+Pt·dxt)
Caso B) Sy aumenta il momento stabilizzante
Il Momento Ribaltante è dato dalle Componenti Orizzontali delle Spinte per la distanza verticale del loro punto di applicazione rispetto al punto di rotazione O.
Mrib = gG1,sfav·Sx·dys
Il Momento Resistente è dato dalla somma del peso proprio del muro più il peso del terreno sovrastante la mensola interna della fondazione per la distanza orizzontale tra il baricentro degli stessi ed il punto di rotazione O più la componente verticale delle spinte per la relativa distanza orizzontale dal punto O.
Mstab = gG1,fav·(Pm·dxp+Pt·dxt+Sy·dxs)
VERIFICA : Ed = Mrib < Rd = Mstab/gr
La verifica Sismica per lo stato limite di ribaltamento viene effettuata analogamente, secondo l’Approccio 2, con la combinazione (A1+M1+R3), ponendo pari all’unità i coefficienti parziali sulle azioni e sui parametri geotecnici (§.7.11.1) e impiegando le resistenze di progetto con i coefficienti parziali gr indicati nella tabella 7.11.III.
Considerando oltre al Peso del muro, del terrapieno e le spiinte statiche, anche le forze di inerzia e l'incremento di spinta sismica
Inoltre, si utilizzano valori di bm incrementati del 50% rispetto a quelli innanzi indicati e comunque non superiori all’unità.
Caso A) Sy dimnuisce il momento ribaltante
Mrib = Kh·(Pm·dyp+Pt·dyt) + Sx·dys-Sy·dxs + DSx·dys - DSy·dxs
Mstab = (1-Kv)·(Pm·dxp+Pt·dxt)
Caso B) Sy aumenta il momento stabilizzante
Mrib = Kh·(Pm·dyp+Pt·dyt) + Sx·dys+ DSx·dys
Mstab = (1-Kv)·(Pm·dxp+Pt·dxt) + Sy·dxs + DSy·dxs
VERIFICA : Ed = Mrib < Rd = Mstab/gr